1-Two Sum#
Given an array of integers, return indices of the two numbers such that they add up to a specific target.
You may assume that each input would have exactly one solution, and you may not use the same element twice.
Example:
1
2
3
4
| Given nums = [2, 7, 11, 15], target = 9,
Because nums[0] + nums[1] = 2 + 7 = 9,
return [0, 1].
|
Brute Force#
1
2
3
4
5
6
7
8
9
10
| public int[] twoSum(int[] nums, int target) {
for (int i=0; i<nums.size; i++){
for (int j=i+1;j<nums.length;j++){
if (nums[j]==target-nums[i]){
return new int[] {i,j};
}
}
}
throw new IllegalArgumentException("No two sum solution");
}
|
Complexity Analysis
1
2
| * Time complexity: O(n^2) we have a nested loop
* Space complexity: O(1) we do not allocate any additional memory
|
One Pass Hash Table#
1
2
3
4
5
6
7
8
9
10
11
| public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
for(int i=0; i<nums.length; i++){
int complement=target-nums[i];
if (map.containsKey(complement)){
return new int[] {map.get(complement),i};
}
map.put(nums[i],i);
}
throw new IllegalArgumentException("No two sum solution");
}
|
Complexity Analysis
1
2
| * Time complexity: O(n) each lookup in the hash table only requires O(1) time
* Space complexity: O(n) we require additional space for the hash table which stores at most n
|
2-Add Two Numbers#
Given two non-empty linked lists representing two non-negative integers with the digits stored in
reverse order and each node containing a single digit, add the two numbers and return as a linked list
Example:
1
2
3
4
| Input (2 -> 4 -> 3) + (5 -> 6 -> 4)
Output 7 -> 0 -> 8
342 + 465 = 807
|
Elementary Math Solution#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| /**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode dummyHead= new ListNode(0);
ListNode p=l1, q=l2, curr=dummyHead;
int carry=0;
while (p!=null||q!=null){
int x= (p!=null) ? p.val :0; //if (p!=null) then x contains p.val
int y= (q!=null) ? q.val :0;
int sum=carry+x+y;
carry=sum/10;
curr.next=new ListNode(sum%10);
curr=curr.next;
if (p!=null) p=p.next;
if (q!=null) q=q.next;
}
if (carry>0){
curr.next= new ListNode(carry);
}
return dummyHead.next;
}
}
|
Complexity analysis
1
2
| * Time Complexity: O(max(m,n)) depends on the lengths of the two linked lists
* Space Complexity: O(max(m,n)) the maximum length of the new list is max(m,n)+1
|
3-Substring No Repeat#
Longest Substring Without Repeating Characters
Given a string find the length of the longest substring without repeating characters.
1
2
3
4
| Example
Input: "abcabcbb"
Output: 3
Explanation: The answer is "abc", with the length of 3
|
1
2
3
4
| Example 2
Input: "bbbbb"
Output: 1
Explanation: The answer is "b", with the length of 1
|
1
2
3
4
5
| Example 3
Input: "pwwkew"
Output: 3
Explanation: The answer is "wke", with the length of 3. Note that the answer must be a substring
"pwke" is a subsequence and not a substring
|
Brute Force#
Algorithm
Suppose we have a function “boolean allUnique(String substring)” which returns true if all the
characters in the substring are unique and false otherwise. We can iterate through all the possible
substrings of the given string s and call the function allUnique. If it turns out to be true, then we
update our answer of the maximum length of substring without duplicate characters.
To enumerate all substrings of a given string we enumerate the start and end indices of them. Suppose
the start and end indices are i and j respectively. Then we have 0 <= i <= j <= n. Thus using two
nested loops with i from 0 to n-1 and j from i+1 to n, we can enumerate all the substrings of s
To check if one string has duplicate characters we can use a set. We iterate through all the
characters in the string and put them into the set one by one. Before putting one character, we check
if the set already contains it. If so we return false and after the loop we return true.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length();
int ans = 0;
for (int i = 0; i < n; i++)
for (int j = i + 1; j <= n; j++)
if (allUnique(s, i, j)) ans = Math.max(ans, j - i);
return ans;
}
public boolean allUnique(String s, int start, int end) {
Set<Character> set = new HashSet<>();
for (int i = start; i < end; i++) {
Character ch = s.charAt(i);
if (set.contains(ch)) return false;
set.add(ch);
}
return true;
}
}
|
Complexity Analysis
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| * Time Complexity: O(n^3) Verifying if characters in [i,j) are unique requires us to scan all of
them which would cost O(j-i) time.
For a given i, the sum of time costed by each j -> [i+1,n] is
"Summation from i+1 to n O(j-1)"
Thus, the sum of all the time consumption is:
O(summation from 0 to n-1(summation from j=i+1 to n (j-1)))
O(summation from i=0 to n-1(1+n-i)(n-i)/2)) = O(n^3)
*Note that the sum of all numbers up to n 1+2+3+...+n = n(n+1)/2
* Space Complexity: O(min(n,m)) We require O(k) space for checking a substring has no duplicate
characters, where k is the size of the set. The size of the Set is
upper bounded by the size of the string n amd the size of the charset
or alphabet m
|
Sliding Window#
A sliding window is an abstract concept commonly used in array/string problems. A window is a range of
elements in the array/string which usually defined by the start and end indices
1
| Ex. [i,j) left-closed, right-open
|
A sliding window is a window that slides its two boundaries in a certain direction, for example if we
slide [i,j) to the right by 1 element, then it becomes [i+1, j+1) - left closed, right open.
Sliding Window approach, whenever we are looking at a section on an array usual to perform calculations
we don’t need to completely recalculate everything for every section of the array. Usually we can use
the value obtained from another section of the array to determine something about this section of the
array. For example if we are calculating the sum of sections of an array we can use the previously
calculated value of a section to determine the sum of an adjacent section in the array.
If we calculate the first section of four values we get 1+2+3+4 = 10 , then to calculate the next section
2+3+4+5 we can just take our first section (window_sum) and perform the operation:
1
| window_sum-first entry + last entry = 10-1+5= 14
|
So essentially for the window sliding technique we use what we know about an existing window to
determine properties for another window.
Algorithm
In the brute force approach, we repeatedly check a substring to see if it has duplicate characters but
this is unnecessary. If a substring from index i to j-1 is already checked to have no duplicate
characters we only need to check if s[j] is already in the substring.
To check if a character is already in the substring we can scan the substring which leads to an O(n^2)
algorithm but we can improve on this runtime using a HashSet as a sliding window to check if a
character exists in the current set O(1).
We use a HashSet to store the characters in the current window [i,j) and then we slide the index j to
the right, if it is not in the HashSet, we slide j further until s[j] is already in the HashSet. At
this point we found the maximum size of substrings without duplicate characters starting with index i.
If we do this for all i, then we obtain our answer.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length();
Set<Character> set = new HashSet<>();
int ans = 0, i = 0, j = 0;
while (i < n && j < n) {
// try to extend the range [i, j]
if (!set.contains(s.charAt(j))){
set.add(s.charAt(j++));
ans = Math.max(ans, j - i);
}
else {
set.remove(s.charAt(i++));
}
}
return ans;
}
}
|
Complexity Analysis
1
2
3
4
5
6
| Time complexity: O(2n)=O(n) Worst case each character will be visited twice by i and j
Space complexity: O(min(m,n)) Same as the brute force method, we need O(k) space for the
sliding window where k is the size of the set. The size of the
set is bounded by the size of the string n and the size of the
charset/alphabet m
|
Sliding Window Optimized#
The previously discussed sliding window approach requires at most 2n steps and this could in fact be
optimized even further to require only n steps. Instead of using a set to tell if a character exists or
not, we could define a mapping of the characters to its index. Then we can skip the characters
immediately when we found a repeated character
If s[j] has a duplicate in the range [i , j) with index j’, we don’t need to increase i little be little
we can just skip all the elements in the range [i , j’] and let i be j’+1 directly
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length(), ans = 0;
Map<Character, Integer> map = new HashMap<>(); // current index of character
// try to extend the range [i, j]
for (int j = 0, i = 0; j < n; j++) {
if (map.containsKey(s.charAt(j))) {
i = Math.max(map.get(s.charAt(j)), i);
}
ans = Math.max(ans, j - i + 1);
map.put(s.charAt(j), j + 1);
}
return ans;
}
}
|
There are two sorted arrays num1 and num2 of size m and n respectively. Find the median of the two
sorted arrays. The overall run time complexity should be O(log (m+n)). You may assume nums1 and nums2
cannot be both empty.
1
2
3
4
5
6
| Example
nums1 = [1, 3]
nums2 = [2]
The median is 2.0
|
1
2
3
4
5
6
| Example 2
nums1= [1, 2]
nums2= [3, 4]
The median is (2+3)/2 = 2.5
|
Recursive Approach#
In statistics the median is used for dividing a set into two equal length subsets with one set being
always greater than the other set. To approach this problem first we cut A into two parts at a random
position i:
1
2
3
| left_A | right_A
A[0], A[1], ... , A[i-1] A[i], A[i+1], ... , A[m-1]
|
Since A has m elements, there are m+1 kinds of cutting as i can range from 0-m. We can also see that
left_A is empty when i is zero and right_A is empty when i=m
1
| len(left_A) = i and len(right_A)= m-i
|
We can similarly cut B into two parts at a random position j:
1
2
3
| left_B | right_B
B[0], B[1], ... , B[j-1] B[j], B[j+1], ... , B[n-1]
|
Now if we put left_A and left_B into one set and put right_A and right_B into another set and name
them left_part and right_part, then we get
1
2
3
| left_part | right_part
A[0], A[1], ... , A[i-1] A[i], A[i+1], ... , A[m-1]
B[0], B[1], ... , B[j-1] B[j], B[j+1], ... , B[n-1]
|
If we can ensure that
- the len(left_part) = len(right_part)
- max(left_part) <= min(right_part)
then we divide all the elements in {A,B} into two parts with equal length and one part is always
greater than the other. Then
1
| median= (max(left_part)+min(right_part))/2
|
To ensure these two conditions, we need to ensure:
- i+j= m-i+n-j (or: m-i+n-j+1) if n>m, we just need to set i=0~m, j= (m+n+1)/2 - i
- B[j-1]<=A[i] and A[i-1]<=B[j]
So, all we need to do is search for i in [0,m] to find an object i such that
B[j-1]<=A[i] and A[i-1]<=B[j] where j=(m+n+1)/2 -i
Then we perform a binary search following the steps described below:
- Set imin=0, imax=0, then start searching in [imin, imax]
- Set i=(imin+imax)/2 , j=(m+n+1)/2 - i
- Now we have len(left_part) = len(right_part) and there are only 3 more situations which we may
encounter:
1
2
3
4
5
6
7
8
9
10
11
| - B[j-1] <= A[i] and A[i-1]<=B[j]
This means that we have found the object i, so we can stop searching
- B[j-1] > A[i]
Means A[i] is too small, we must adjust i to get B[j-1]<=A[i] so we increase i because this will
cuase j to be decreased. We cannot decrease i because when i is decreased, j will be increased
so B[j-1] is increased and A[i] is decreased (B[j-1]<= A[i] will never be satisfied)
- A[i-1] > B[j]
Means A[i-1] is too big and thus we must decrease i to get A[i-1]<=B[j]. In order to do that we
must adjust the searching range to [imin, i-1] so we set imax=i-1 and go back to step 2
|
When the object i is found, then the media is:
max(A[i-1],B[j-1]), when m+n is odd
(max(A[i-1],B[j-1])+min(A[i],B[j]))/2, when m+n is even
Next is to consider the edge values i=0, i=m, j=0, j=n where A[i-1], B[j-1], A[i], B[j] may not exist
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| class Solution {
public double findMedianSortedArrays(int[] A, int[] B) {
int m=A.length;
int n=B.length;
if (m>n) { //ensuring that m<=n
int[] temp=A; A=B; B=temp;
int tmp=m; m=n; n=tmp;
}
int iMin=0, iMax=m, halfLen=(m+n+1)/2;
while (iMin<=iMax) {
int i=(iMin+iMax)/2
int j= halfLen - i;
if (i<iMax && B[j-1] > A[i]){
iMin=i+1; //i is too small
}
else if (i>iMin && A[i-1]>B[j]) {
iMax=i-1; //i is too big
}
else{ //we have found the object i
int maxLeft=0;
if (i==0) {
maxLeft=B[j-1];
}
else if (j==0){
maxLeft=A[i-1];
}
else{
maxLeft=Math.max(A[i-1], B[j-1]);
}
if ((m+n)%2 ==1) {
return maxLeft;
}
int minRIght=0;
if (i==m) {
minRight=B[j];
}
else if (j==n) {
minRight=A[i];
}
else {
minRight=Math.min(B[j], A[i]);
}
return (maxLeft+minRight)/2.0;
}
}
return 0.0;
}
}
|
Complexity Analysis
1
2
3
4
5
6
7
8
| Time Complexity: O(log(min(m,n))) At first the searching range is [0,m] and the length of this
searching range will be reduced by half after each loop so we
only need log(m) loops. Since we do constant operations in
each loop the time complexity is O(log(m) and since m<=n the
time complexity is O(log(min(m,n))
Space Complexity: O(1) We only need constant memory to store 9 local variables so the
space complexity is O(1)
|
5-Longest Palindromic Substring#
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length
of s is 1000.
1
2
3
4
5
6
| Example 1:
Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer
|
1
2
3
4
| Example 2:
Input: "cbbd"
Output: "bb"
|
Longest Common Substring#
Some people will be tempted to come up with this quick solution which is unforunately flawed, “reverse
S and become S’. Find the longest common substring between S and S’ and that will be the longest
palindromic substring.” This will work with some examples but there are some cases where the longest
common substring is not a valid palindrome.
Ex. S="abacdfgdcaba", S'="abacdgfdcaba"
The longest common substring between S and S’ is “abacd” and clearly this is not a valid
palindrome
We can solve this problem however by checking if the substring’s indices are the same as the reversed
substring’s original indices each time we find a longest common substring. If it is, then we attempt
to update the longest palindrome found so far, if not we skip this and find the next candidate
Complexity Analysis
1
2
| Time Complexity: O(n^2)
Space Complexity: O(n^2)
|
Brute Force#
The obvious brute force solution is to pick all possible starting and ending position for a substring
and verify if it is a palindrome
Complexity Analysis
1
2
3
4
5
| Time Complexity: O(n^3) If n is the length of the input string, there are a total of
(n 2) = n(n-1)/2 substrings and since verifying each substring takes
O(n) time, the run time complexity is O(n^3)
Space Complexity: O(1)
|
Dynamic Programming#
We can improve on the brute force solution by avoid some unnecessary re-computation while validating
palidromes. Consider the word “ababa”, if we already know that “bab” is a palindrome then we can
determine that ababa is a palindrome by noticing that the two left and right letters connected to bab
are the same.
This yields a straight forward dynamic programming solution where we initialize the one and two letters
palindromes and then work our way up finding all three letters palindromes and so on.
Complexity Analysis
1
2
3
| Time Complexity: O(n^2)
Space Complexity: O(n^2) Using O(n^2) space to store the table
|
Expand Around Center#
This approach allows us to solve this problem in O(n^2) time using only constant space complexity. We
observe that a palindrome mirrors around its enter and therefore a palindrome can be expanded from its
center and there are only 2n-1 such centers (for palindromes with an even number of letters like
“abba” its center is in between two letters).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public String longestPalindrome(String s) {
if (s==null || s.length() < 1) return ""; //edge case
int start=0, end=0;
for (int i=0; i<s.length(); i++) {
int len1=expandAroundCenter(s,i,i);
int len2=expandAroundCenter(s,i,i+1);
int len=Math.max(len1,len2);
if (len>end-start) {
start= i-(len-1)/2;
end=i+len/2
}
}
return s.substring(start,end+1);
}
private int expandAroundCenter(String s, int left, int right) {
int L=left, R=right;
while(L>=0 && R<s.length() && s.charAt(L)==s.charAt(R)) {
L--;
R++;
}
return R-L-1;
}
|
Manacher’s Algorithm#
There is an O(n) algorithm called Manacher’s algorithm, however, it is a non-trivial algorithm and no
one would expect you to come up with this algorithm in a 45 minute coding session
6-ZigZag Conversion#
The string “PAYPALISHIRING” is written in a zigzag pattern on a given number of rows like this:
1
2
3
| P A H N
A P L S I I G
Y I R
|
And then read line by line: “PAHNAPLSIIGYIR”. Write a code that will take a string and make this
conversion given a number of rows:
1
| string convert(string s, int numRows);
|
1
2
3
4
| Example 1:
Input: s="PAYPALISHIRING", numRows=3
Output: "PAHNAPLSIIGYIR"
|
1
2
3
4
5
6
7
8
9
10
11
| Example 2:
Input: s="PAYPALISHIRING", numRows=4
Output: "PINALSIGYAHRPI"
Explanation:
P I N
A L S I G
Y A H R
P I
|
Sort by Row#
By iterating through the string from left to right we can easily determine which row in the Zig-Zag
pattern that a character belongs to
Algorithm
We can use min(numRows,len(s)) lists to represent the non-empty rows of the Zig-Zag Pattern.
Iterate through s from left to right appending each character to the appropriate row. The appropriate
row can be tracked using two variables: the current row and the current direction.
The current direction only changes when we moved to the topmost row or moved down to the bottommost
row
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public String convert(String s, int numRows) {
if (numRows==1) return s; //if there is only one row return string
List<StringBuilder> rows=new ArrayList<>();
for (int i=0; i<Math.min(numRows, s.length()); i++){
rows.add(new StringBuilder());
}
int curRow=0;
boolean goingDown=false;
for(char c: s.toCharArray()) {
rows.get(curRow).append(c);
if (curRow==0 || curRow==numRows-1) {
goingDown=!goingDown;
}
curRow+=goingDown ? 1 : -1;
}
StringBuilder ret= new StringBuilder();
for(StringBuilder row:rows) {
ret.append(row);
}
return ret.toString();
}
}
|
Complexity Analysis
1
2
| Time Complexity: O(n) where n==len(s)
Space Complexity: O(n)
|
Visit by Row#
Visit the characters in the same order as reading the Zig-Zag pattern line by line
Algorithm
Visit all characters in row 0 first, then row 1, then row 2, and so on.
For all whole numbers k,
* characters in row 0 are located at indexes k*(2*numRows-2)
* characters in row numRows -1 are located at indexes k*(2*numRows-2)+ numRows -1
* characters in inner row i are located at indexes k*(2*numRows-2)+i and (k+1)(2*numRows-2)-i
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public String convert(String s, int numRows) {
if (numRows==1) return s;
StringBuilder ret=new StringBuilder();
int n=s.length();
int cycleLen= 2* numRows -2;
for (int i=0; i<numRows; i++) {
for (int j=0; j+1<n; j+= cycleLen) {
ret.append(s.charAt(j+i));
if (i!=0 && i!=numROws-1 && j+cycleLen-i<n) {
ret.append(s.charAt(j+cycleLen-i));
}
}
return ret.toString();
}
}
}
|
Complexity Analysis
1
2
3
4
| Time Complexity: O(n) where n==len(s) Each index is visited once
Space Complexity: O(n) C++ implementation can achieve O(1) if the return string is not considered
extra space
|
7-Reverse Integer#
Given a 32- bit signed integer, reverse digits of an integer.
1
2
3
4
| Example 1:
Input: 123
Output: 321
|
1
2
3
4
| Example 2:
Input: -123
Output: -321
|
1
2
3
4
| Example 3:
Input: 120
Output: 21
|
For the purpose of this problem assume that your function returns 0 when the reversed integer overflows
Pop and Push Digits and Check Before Overflow#
We can build up the reverse integer one digit at and time and before doing so we can check whether or
not appedning another digit would cause overflow
Algorithm
Reversing an integer can be done similarly to reversing a string. We want to repeatedly “pop” the last
digit off of x and push it to the back of the rev so that in the end rev is the reverse of x.
To push and pop digits without the help of some auxiliar stack/array we can use math
1
2
3
4
5
6
7
| //pop operation:
pop = x%10;
x/=10;
//push operation:
temp=rev*10+pop;
rev =temp;
|
This statement is dangerous however as the statement temp=rev*10+pop may cause an overflow and luckily
it is easy to check beforehand whether or not this statement would cause an overflow.
- If temp=rev*10+pop causes an overflow, then rev>=INTMAX/10
- If rev> INTMAX/10, then temp=rev*10+pop is guaranteed to overflow
- if rev==INTMAX/10, then temp=rev*10 + pop will overflow if an only if pop>7
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public int reverse(int x) {
int rev=0;
while (x!=0) {
int pop=x%10;
x/=10;
if (rev>Integer.MAX_VALUE/10||(rev==Integer.MAX_VALUE/10 && pop>7)) return 0;
if (rev<Integer.MIN_VALUE/10||(rev==Integer.MIN_VALUE/10 && pop<-8)) return 0;
rev=rev*10 +pop;
}
return rev;
}
}
|
Complexity Analysis
1
2
| Time Complexity: O(log(x)) There are roughly log10(x) digits in x
Space Complexity: O(1)
|
8-String to Integer (atoi)#
Implement atoi which converts a string to an integer
The function first discards as many whitespace characters as necessary until the first non-whitespace
character is found. Then, starting from this character, takes an optional initial plus or minus sign
followed by as many numerical digits as possible and interprets them as a numerical value.
The string can contain additional characters after those that form the integral number, which are
ignored and have no effect on the behavior of this function.
If the first sequence of non-whitespace characters in str is not a valid integral number, or if no such
sequence exits because either str is empty or it contains only whitespace characters, no conversion is
performed.
If no valid conversion could be performed a zero value is returned
Note:
- only the space character ’ ’ is considered as whitespace character
- assume we are dealing with an environment which could only store integers within the 32-bit signed integer range: [-2^31, 2^31-1]. If the numerical value is out of the range of representable values, INT_MAX (2^31-1) or INT_MIN (-2^31) is returned
1
2
3
4
| Example 1:
Input: "42"
Output: 42
|
1
2
3
4
| Example 2:
Input: " -42"
Output: -42
|
1
2
3
4
| Example 3:
Input: "4193 with words "
Output: 4193
|
1
2
3
4
| Example 4:
Input: "words and 987"
Output: 0
|
1
2
3
4
| Example 5:
Input: "-91283472332"
Output: -2147483648 //out of the range of a 32-bit signed integer so INT_MIN is returned
|
ASCII Conversion#
Recognize that ASCII characters are actually numbers and 0-9 digits are numbers starting from decimal
48 (0x30 hexadecimal)
1
2
3
4
| '0' is 48
'1' is 49
...
'9' is 57
|
So to get the value of any character digit you can just remove the ‘0’
1
2
| '1' - '0' => 1
49 - 48 => 1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| public int myAtoi(String str) {
int index=0, sign=1, total=0;
//1. Empty string
if (str.length() ==0) return 0;
//2. Remove Spaces
while(str.charAt(index)==' ' && index < str.length())
index++;
//3. Handle signs
if (str.charAt(index)=='+' || str.charAt(index)=='-'){
sign= str.charAt(index) == '+' ? 1:-1;
index++;
}
//4. COnvert number and avoid overflow
while(index<str.length()){
int digit= str.charAt(index) - '0';
if (digit<0||digit>9) break;
//check if total will overflow after 10 times and add digit
if (Integer.MAX_VALUE/10 < total || Integer.MAX_VALUE/10 == total
&& Integer.MAX_VALUE%10<digit) {
return sign==1 ? Integer.MAX_VALUE : Integer.MIN_VALUE;
}
total= 10* total+digit;
index++;
}
return total*sign;
}
|
9-Palindrome Number#
Determines whether an interger is a palindrome. An integer is a palindrome when it reads the same
backward as forward.
1
2
3
4
| Example 1:
Input: 121
Output: true
|
1
2
3
4
5
6
| Example 2:
Input: -121
Output: false
Explanation: From left to right, it reads -121, meanwhile from right to left it becomes 121- .
Therefore it is not a palindrome
|
1
2
3
4
5
| Example 3:
Input: 10
Output: false
Explanation: Reads 01 from right to left. Therefore it is not a palindrome
|
Revert Half of the Number#
A first idea which may come to mind is to convert the number into a string and check if the string is a
palindrome but this would require extra non-constant space for creating the string not allowed by the
problem description
Second idea would be reverting the number itself and comparing the number with the original number, if
they are the same then the number is a palindrome, however if the reversed number is larger than
int.MAX we will hit integer overflow problem.
To avoid the overflow issue of the reverted number, what if we only revert half of the int number? The
reverse of the last half of the palindrome should be the same as the first half of the number if the
number is a palindrome.
If the input is 1221, if we can revert the last part of the number “1221” from “21” to “12” and compare
it with the first half of the number “12”, since 12 is the same as 12, we know that the number is a
palindrome.
Algorithm
At the very beginning we can deal with some edge cases. All negative numbers are not palindrome and
numbers ending in zero can only be a palindrome if the first digit is also 0 (only 0 satisfies this
property)
Now let’s think about how to revert the last half of the number. For the number 1221 if we do 1221%10
we get the last digit 1. To get the second last digit we divide the number by 10 1221/10=122 and then
we can get the last digit again by doing a modulus by 10, 122%10=2. If we multiply the last digit by
10 and add the second last digit 1*10+2=12 which gives us the reverted number we want. COntinuing this
process would give us the reverted number with more digits.
Next is how do we know that we’ve reached the half of the number?
Since we divided the number by 10 and multiplied the reversed number by 10 when the original number is
less than the reversed number, it means we’ve gone through half of the number digits.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public boolean isPalindrome(int x) {
if (x<0 || (x%10==0 && x!=0)) {
return false;
}
int revertedNumber=0;
while (x>revertedNumber){
revertedNumber=x%10+revertedNumber*10;
x/=10;
}
//when the length is an odd number, we can get rid of the middle digit by
//revertedNumber/10
//For example when the input is 12321, at the end of the while loop we get x=12,
//revertedNumber=123, since the middle digit doesn't matter in a palindrome we can
//simply get rid of it
return x==revertedNumber||x==revertedNumber/10;
}
}
|
10-Regular Expression Matching#
Given an input string (s) and a pattern (p), implement regular expression matching with support for ‘.’
and ‘*’
1
2
| '.' Matches any single character
'*' Matches zero or more of the preceding element
|
The matching should cover the entire input string (not partial)
Note:
- s could be empty and contains only lower case letters a-z
- p could be empty and contains only lower case letters a-z and characters like . or *
1
2
3
4
5
6
7
| Example 1:
Input:
s="aa"
p="a"
Output: false
Explanation: "a" does not match the entire string "aa"
|
1
2
3
4
5
6
7
8
| Example 2:
Input:
s="aa"
p="a*"
Output: true
Explanation: '*' means zero of more of the preceding element, 'a'. Therefore, by repeating
'a' once it becomes "aa"
|
1
2
3
4
5
6
7
| Example 3:
Input:
s="ab"
p=".*"
Output: true
Explanation: '.*' means "zero or more (*) of any character (.)"
|
1
2
3
4
5
6
7
8
| Example 4:
Input:
s="aab"
p="c*a*b"
Output: true
Explanation: c can be repeated 0 times, a can be repeated 1 time. Therefore it matches
"aab"
|
1
2
3
4
5
6
| Example 5:
Input:
s="mississippi"
p="mis*is*p*."
Output: false
|
Recursion#
If there were no Kleene stars (the * wildcard characters for regular expressions), the problem would
be easier- we simply check from left to right if each character of the text matches the pattern. When
a star is present we may need to check for may different suffixes of the text and see if they match
the rest of the pattern. A recursive solution is a straightforward way to represent this relationship
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public boolean isMatch(String text, String pattern) {
if (pattern.isEmpty()) return text.isEmpty();
boolean first_match=(!text.isEmpty() &&
(pattern.charAt(0)==text.charAt(0) || pattern.charAt(0)=='.'));
if (pattern.length()>=2 && pattern.charAt(1) =='*'){
return (isMatch(text,pattern.substring(2))||
(first_match && isMatch(text.substring(1),pattern)));
//note: pattern.substring(2) returns all of the characters after index 2 of pattern
}
else {
return first_match && isMatch(text.substring(1), pattern.substring(1));
}
}
}
|
Complexity Analysis
1
2
3
4
5
6
7
8
9
10
11
12
13
| Time Complexity: Let T, P be the lengths of the text and the pattern respectively. In the worst
case, a call to match(text[i:],pattern[2j:]) will be made (i+j i) times, and
strings of the order O(T-i) and O(P-2*j) will be made. Thus the complexity has
the order:
summation from i=0 to T * summation from j=0 to P/2 * (i+j i) O(T+P-i-2j).
We can show that this is bounded by O((T+P)2^(T+P/2))
Space Complexity: For every call to match, we will create those strings as described above
possibly creating duplicates. If memory is not freed, this will also take a
total of O((T+P)2^(T+P/2)) space even though there are only order O(T^2+P^2)
unique suffixes of P and T that are actually required
|
Dynamic Programming#
As the problem has an optimal substructure, it is natural to cache intermediate results. We ask the
question dp(i,j): does text[i:] and pattern[j:] match? We can describe our answer in terms of answers
to questions involving smaller strings
Algorithm
We proceed with the same recursion as in Approach 1, except because calls will only ever be made to
match(text[i:], pattern[j:]), we use dp(i,j) to handle those calls instead, saving us expensive
string-building operations and allowing us to cache the intermediate results
Java Top-Down Variation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| enum Result {
TRUE, FALSE
}
class Solution {
Result[][] memo;
public boolean isMatch(String text, String pattern) {
memo=new Result[text.length() +1][pattern.length() +1];
return dp(0,0,text,pattern);
}
public boolean dp(int i, int j, String text, String pattern) {
if (memo[i][j]!=null) {
return memo[i][j]==Result.TRUE;
}
boolean ans;
if (j==pattern.length()){
ans=i==text.length();
}
else {
boolean first_match=(i<text.length() && (pattern.charAt(j) == text.charAt(i) ||
patter.charAt(j) == '.'));
if (j+1<pattern.length() && pattern.charAt(j+1)=='*'){
ans=(dp(i,j+1,text,pattern)||first_match&& dp(i+1,j,text,pattern));
}
else {
ans=first_match && dp(i+1, j+1, text, pattern);
}
}
memo[i][j]=ans? Result.TRUE: Result.FALSE;
return ans;
}
}
|
Complexity Analysis
1
2
3
4
5
| Time Complexity: Let T, P be the lengths of the text and the pattern respectively. The work
for every call to dp(i,j) for i=0,...,T; j=0,...,P is done once and it is O(1) work. Hence the time complexity is O(TP)
Space Complexity: The only memory we use is the O(TP) boolean entries in our cache. Hence, the
space complexity is O(TP)
|
Non-Recursive#
The recursive programming solutions are pretty confusing so this implementation uses 2D arrays and
Dynamic Programming
The logic works as follows:
1
2
3
4
5
6
7
8
9
10
11
| 1. If p.charAt(j) == s.charAt(i) : dp[i][j] = dp[i-1][j-1];
2. If p.charAt(j) == '.' : dp[i][j] = dp[i-1][j-1];
3. If p.charAt(j) == '*':
Subconditions
1. If p.charAt(j-1)!= s.charAt(i):dp[i][j]=dp[i][j-2] //in this case a* only counts as empty
2. If p.charAt(i-1)== s.charAt(i) or p.charAt(i-1) == '.':
dp[i][j] = dp[i-1][j] //in this case a* counts as multiple a
or dp[i][j] = dp[i][j-1] //in this case a* counts as single a
or dp[i][j] = dp[i][j-2] //in this case a* counts as empty
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| public boolean isMatch(String s, String p) {
if (s==null || p==null){
return false;
}
boolean[][] dp=new boolean[s.length()+1][p.length()+1];
dp[0][0]=true;
for (int i=0;i<p.length(); i++){
if (p.charAt(i)=='*' && dp[0][i-1]){
dp[0][i+1]=true;
}
}
for (int i=0;i<s.length();i++){
for (int j=0;j<p.length();j++){
if (p.charAt(j)=='.'){
dp[i+1][j+1]=dp[i][j];
}
if (p.charAt(j)==s.charAt(i)){
dp[i+1][j+1]=dp[i][j];
}
if (p.charAt(j)=='*'){
if (p.charAt(j-1)!=s.charAt(i) && p.charAt(j-1) !='.'){
dp[i+1][j+1]=dp[i+1][j-1];
}
else{
dp[i+1][j+1]=(dp[i+1][j] || dp[i][j+1] || dp[i+1][j-1]);
}
}
}
}
return dp[s.length()][p.length()];
}
|
11-Container with the Most Water#
Given n non negative integers a1,a2, … , an where each represents a point at coordinate (i, ai). n
vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two
lines, which together with x-axis forns a container such that the container contains the most water.
1
2
3
4
5
|
^ ^
These two values form the container which could hold water at a max height of 7, these values
are also 7 array indexes apart from each other so it could hold water at a max width of 7. The
area of water which could be held is thus 7 x 7 = 49
|
Brute Force#
In this case we simply consider the area for every possible pair of the lines and find out the maximum
area out of those.
1
2
3
4
5
6
7
8
9
10
11
| public class Solution {
public int maxArea(int[] height) {
int maxarea=0;
for (int i=0; i<height.length; i++){
for (int j=i+1;j<height.length;j++){
maxarea=Math.max(maxarea, Math.min(height[i],height[j])*(j-i));
}
}
return maxarea;
}
}
|
Complexity Analysis
1
2
| Time complexity: O(n^2) Calculating the area for all n(n-1)/2 height pairs
Space complexity: O(1) Constant extra space is used
|
Two Pointer Approach#
The intuition behind this approach is that the area formed between the lines will always be limited by
the height of the shorter line. Further, the farther the lines, the more will be the area obtained.
We take two pointers, one at the beginning and one at the end of the array constituting the length of
the lines. Further, we maintain a variable maxarea to store the maximum area obtained till now. At
every step, we find out the area formed between them, update maxarea and move the pointer pointing to
the shorter line towards the other end by one step.
Initially we consider the area constituting the exterior most lines. Now to maximize the area we need
to consider the area between the lines of larger lengths. If we try to move the pointer at the longer
line inwards, we won’t gain any increase in area, since it is limited by the shorter line. But moving
the shorter line’s pointer could turn out to be benefical, as per the same argument, despite the
reduction in width. This is done since a relatively longer line obtained by moving the shorter line’s
pointer might overcome the reduction in area caused by the width reduction.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public class Solution {
public int maxArea(int[] height) {
int maxarea=0, l=0, r=height.length-1;
while (l<r){
maxarea=Math.max(maxarea,Math.min(height[l],height[r])*(r-l));
if (height[l]<height[r]){
l++;
}
else{
r--;
}
}
return maxarea;
}
}
|
Complexity Analysis
1
2
| Time complexity: O(n) Single pass
Space complexity: O(1) Constant space is used
|
12-Integer To Roman#
Roman numerals are represented by seven different symbols: I, V, X, L, C, D and M
1
2
3
4
5
6
7
8
| Symbol Value
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
|
For example, two is written as II in Roman numeral, just two one’s added together. Twelve is written as
XII which is simply X + II. The number twenty seven is written as XXVII, which is XX + V + II.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for
four is not IIII. Instead, the number four is written as IV. Because the one is before the five we
subtract it making four. The same principle applies to the number nine which is written as IX. There
are six instances where subtraction is used:
- I can be placed before V (5) and X (10) to make 4 and 9
- X can be placed before L (50) and C(100) to make 40 and 90
- C can be placed before D (500) and M(1000) to make 400 and 900
Given an integer, convert it to a roman numeral, input is guaranteed to be within the range from
1 to 3999
1
2
3
4
| Example 1:
Input: 3
Output: "III"
|
1
2
3
4
| Example 2:
Input: 4
Output: "IV"
|
1
2
3
4
| Example 3:
Input: 9
Output: "IX"
|
1
2
3
4
5
| Example 4:
Input: 58
Output: "LVIII"
Explanation: L=50, V=5, III=3
|
1
2
3
4
5
| Example 5:
Input: 1994
Output: "MCMXCIV"
Explanation: M=1000, CM=900, XC=90 and IV=4
|
String Array#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public static String intToRoman(int num) {
String M[]={"", "M", "MM", "MMM"};
//represents 1000, 2000, and 3000 since we know the number is in the range 1 to 3999
String C[]={"", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"};
//represents 0, 100, 200, 300, 400, 500, 600, 700, 800, 900
String X[]={"", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"};
//represents 0, 10, 20, 30, 40, 50, 60, 70, 80, 90
String I[]={"", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"};
//represents 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
return M[num/1000] + C[(num%1000)/100] + X[(num%100)/10] + I[num%10];
}
|
13-Roman to Integer#
Roman numerals are represented by seven different symbols I, V, X, L, C, D and M
1
2
3
4
5
6
7
8
| Symbol Value
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
|
For example, two is written as II in Roman numeral, just two one’s added together. Twelve is written as
XII which is simply X + II. The number twenty seven is written as XXVII, which is XX + V + II.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for
four is not IIII. Instead, the number four is written as IV. Because the one is before the five we
subtract it making four. The same principle applies to the number nine which is written as IX. There
are six instances where subtraction is used:
- I can be placed before V (5) and X (10) to make 4 and 9
- X can be placed before L (50) and C(100) to make 40 and 90
- C can be placed before D (500) and M(1000) to make 400 and 900
Given an integer, convert it to a roman numeral, Input is guaranteed to be within the range from
1 to 3999
1
2
3
4
| Example 1:
Input: "III"
Output: 3
|
1
2
3
4
| Example 2:
Input: "IV"
Output: 4
|
1
2
3
4
| Example 3:
Input: "IX"
Output: 9
|
1
2
3
4
5
| Example 4:
Input: "LVIII"
Output: 58
Explanation: L=50, V=5, III=3
|
1
2
3
4
5
| Example 5:
Input: "MCMXCIV"
Output: 1994
Explanation: M=1000, CM=900, XC=90 and IV=4
|
Character Array#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public int romanToInt(String s) {
Map<Character, Integer> map = new HashMap();
map.put('I', 1);
map.put('V', 5);
map.put('X', 10);
map.put('L', 50);
map.put('C', 100);
map.put('D', 500);
map.put('M', 1000);
char[] sc= s.toCharArray();
int total= map.get(sc[0]);
int pre=map.get(sc[0]);
for (int i=1; i<sc.length; i++) {
int curr=map.get(sc[i]);
if (curr<=pre) {
total= total + curr;
}
else {
total=total+curr -2*pre;
}
pre=curr;
}
return total;
}
}
|
14-Longest Common Prefix#
Write a function to find the longest common prefix string amongst an array of strings. If there is no
common prefix, return an empty string ""
1
2
3
4
| Example 1:
Input: ["flower", "flow", "flight"]
Output: "fl"
|
1
2
3
4
5
6
| Example 2:
Input: ["dog", "racecar", "car"]
Output: ""
Explanation: There is no common prefix among the input strings
|
Note:
All given inputs are in lowercase letters a-z
Horizontal Scanning#
*Intuition:*
For a start we will describe a simple way of find the longest prefix shared by a set of strings
LCP(S1 … Sn).We will use the observation that:
1
| LCP(S1 ... Sn) = LCP(LCP(LCP(S1, S2), S3), ... Sn)
|
Algorithm:
To employ this idea, the algorithm iterates through the strings [S1 … Sn]. finding at each iteration
i the longest common prefix of strings LCP(S1 … Si). When LCP(S1 … Si) is an empty string, the
algorithm ends. Otherwise after n iterations, the algorithm returns LCP(S1 … Sn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
Example:
{leets, leetcode, leet, leeds}
\ /
LCP{1,2} = leets
leetcode
leet
\ {leets, leetcode, leet, leeds}
\ /
LCP{1,3} = leet
leet
leet
\ {leets, leetcode, leet, leeds}
\ /
LCP{1,4} leet
leeds
lee
LCP{1,4} = "lee"
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public String longestCommon Prefix(String[] strs){
if (strs.length==0){
return "";
}
String prefix=strs[0];
for (int i=1; i<strs.length; i++) {
while (strs[i].indexOf(prefix) != 0) {
prefix=prefix.substring(0, prefix.length() -1);
if (prefix.isEmpty()) {
return "";
}
}
return prefix;
}
}
|
Complexity Analysis
1
2
3
4
5
6
| Time complexity: O(S) Where S is the sum of all characters in all strings. In the worse case
all n strings are the same. The algorithm compares the string S1 with
the other strings [S2 ... Sn]. There are S character comparisons where
S is the sum of all characters in the input array
Space complexity: O(1) We only used constant extra space
|
Vertical Scanning#
Imagine a very short string is at the end of the array. The above approach will still do S comparisons.
One way to optimize this case is to do vertical scanning. We compare characters from top to bottom on
the same column (same character index of the strings) before moving on to the next column.
1
2
3
4
5
6
7
8
9
10
11
12
| public String longestCommonPrefix(String[] strs) {
if (strs==null || strs.length==) return "";
for (int i=0; i<strs[0].length(); i++){
char c=strs[0].charAt(i);
for (int j=1; j<strs.length; j++) {
if (i==strs[j].length() || strs[j].charAt(i)!=c){
return strs[0].substring(0,i);
}
}
}
return strs[0];
}
|
Complexity Analysis
1
2
3
4
5
6
7
| Time complexity: O(S) Where S is the sum of all characters in all strings. In the worst case
there will be n equal strings with length m and the algorithm performs
S=n*m character comparisons. Even the worst case is still the same as
Approach 1, in the best case there are at most n*minLen comparisons
where minLen is the length of the shortest string in the array.
Space complexity: O(1) We only used constant extra space
|
Divide and Conquer#
The idea of the algorithm comes from the associative property of LCP operation. We notice that:
LCP(S1 … Sn) = LCP(LCP(S1 … Sk), LCP(Sk+1 … Sn)), where LCP(S1 … Sn) is the longest common
prefix in a set of strings [S1 … Sn], 1<k<n
Algorithm
To apply the previous observation, we use the divide and conquer technique, where we split the
LCP(Si … Sj) problem into two subproblems LCP(Si … Smid) and LCP(Smid+1 … Sj), where mid is
(i+j)/2. We use their solutions lcpLeft and lcpRight to construct the solution of the main problem
LCP(Si … Sj). To accomplish this we compare one by one the characters of lcpLeft and lcpRight till
there is no character match. The found common prefix of lcpLeft and lcpRight is the solution of the
LCP(Si … Sj)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| {leetcode, leet, lee, le}
/ \
Divide {leetcode, leet} {lee, le}
Conquer | |
{leet} {le}
\ /
{le}
Searching for the longest common prefix (LCP) in dataset {leetcode, leet, lee, le}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length ==0) return "";
return longestCommonPrefix(strs, 0, strs.length-1);
}
private String longestCommonPrefix(String[] strs, int l, int r) {
if (l==r) {
return strs[l];
}
else {
int mid=(l+r)/2;
String lcpLeft= longestCommonPrefix(strs,l, mid);
String lcpRight= longestCommonPrefix(strs,mid+1;r);
return commonPrefix(lcpLeft,lcpRight);
}
}
String commonPrefix(String left, String right) {
int min=Math.min(left.length(), right.length());
for (int i=0; i<min; i++) {
if (left.charAt(i) !=right.charAt(i) ){
return left.substring(0, i);
}
}
return left.substring(0, min);
}
|
Complexity Analysis
In the worst case we have n equal strings with length m
1
2
3
4
5
6
7
8
| Time Complexity: O(S) where S is the number of all characters in the array, S=m*n so time
complexity is 2*T(n/2)+O(m). Therefore time complexity is O(S). In the
best case the algorithm performs O(minLen * n) comparisons, where
minLen is the shortest string of the array
Space Complexity: O(m*log(n)) There is a memory overhead since we sotre recursive call in the
execution stack. There are log(n) recursive calls, each store needs m
space to store the result so space complexity is O(m*log(n))
|
Binary Search#
The idea is to apply binary search method to find the string with maximum value L, which is common
prefix of all the strings. The algorithm searches the space in the interval (0 … minLen), where
minLen is minimum string length and the maximum possible common prefix. Each time search space is
divided in two equal parts, one of them is discarded because it is sure that it doesn’t contain the
solution. There are two possible cases:
- S[1…mid] is not a common string. This means that for each j>i, S[1…j] is not a common string and we discard the second half of the search space
- S [1…mid] is common string. This means that for each i<j, S[1…i] is a common string and we discard the first half of the search space, because we try to find longer common prefix
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| {leets, leetcode, leetc, leeds}
|
"leets"
/ \
"lee" "ts"
midpoint
"lee" in "leetcode" : yes
"lee" in "leetc" : yes
"lee" in "leeds" : yes
|
"leets"
/ \
"lee" "ts"
| / \
"lee" "t" "s"
midpoint
"leet" in "leetcode" : yes
"leet" in "leetc" : yes
"leet" in "leeds" : no
LCP= "lee"
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public String longestCommonPrefix(String[] strs) {
if (strs==null || strs.length==0)
return "";
int minLen=Integer.MAX_VALUE;
for (String str: strs)
minLen=Math.min(minLen, str.length());
int low=1;
int high=min Len;
while (low<=high) {
int middle=(low+high)/2;
if (isCommonPrefix(strs, middle)
low=middle+1;
else
high=middle-1;
}
return strs[0].substring(0, (low + high)/2);
}
private boolean isCommonPrefix(String[] strs, int len) {
String str1=strs[0].substring(0,len);
for (int i=1; i<strs.length; i++)
if (!strs[i].startsWith(str1))
return false;
return true;
}
|
**Complexity Analysis
In the worst case we have n equal strings with length m
1
2
3
4
5
| Time complexity: O(S * log(n)), where S is the sum of all characters in all strings. The
algorithm makes log(n) iterations, for each of them there are S=m*n
comparisons, which gives in total O(S * log(n)) time complexity
Space complexity: O(1). We only used constant extra space
|
Further Thoughts#
Considering a slightly different problem:
1
2
| Given a set of keys S= [S1, S2 ... Sn], find the longest common prefix among a string q and S.
This LCP query will be called frequently
|
We coule optimize LCP queries by storing the set of keys S in a Trie. See this for Trie
implementation. In a Trie, each node descending from the root represents a common prefix of some keys. But we need to
find the longest common prefix of a string q and all key strings. This means that we have to find the
deepest path from the root, which satisfies the following conditions
- it is a prefix of query string q
- each node along the path must contain only one child element. Otherwise the found path will not be a
common prefix among all strings
- the path doesn’t comprise of nodes which are marked as end of key. Otherwise the path couldn’t be a
prefix of a key which is shorter than itself
Algorithm
The only question left is how to find the deepest path in the Trie, that fulfills the requirements
above. The most effective way is to build a trie from {S1 … Sn] strings. Then find the prefix of
query string q in the Trie. We traverse the Trie from the root, till it is impossible to continue the
path in the Trie because one of the conditions above is not satisfied.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| Searching for the longest common prefix of string "le" in a Trie from dataset {lead, leet}
Root
1
l ===========> \ l
2
e ===============> \ e
LCP "le" FOUND =============> 3
a / \ e End of Key "lee"
6 4
d / \ t
END OF KEY "lead" 7 5 End of key "leet"
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| public String longestCommonPrefix(String q, String[] strs) {
if (strs == null || strs.length == 0)
return "";
if (strs.length == 1)
return strs[0];
Trie trie = new Trie();
for (int i = 1; i < strs.length ; i++) {
trie.insert(strs[i]);
}
return trie.searchLongestPrefix(q);
}
class TrieNode {
// R links to node children
private TrieNode[] links;
private final int R = 26;
private boolean isEnd;
// number of children non null links
private int size;
public void put(char ch, TrieNode node) {
links[ch -'a'] = node;
size++;
}
public int getLinks() {
return size;
}
//assume methods containsKey, isEnd, get, put are implemented as it is described
//in )
}
public class Trie {
private TrieNode root;
public Trie() {
root = new TrieNode();
}
//assume methods insert, search, searchPrefix are implemented
private String searchLongestPrefix(String word) {
TrieNode node = root;
StringBuilder prefix = new StringBuilder();
for (int i = 0; i < word.length(); i++) {
char curLetter = word.charAt(i);
if (node.containsKey(curLetter) && (node.getLinks() == 1) && (!node.isEnd())) {
prefix.append(curLetter);
node = node.get(curLetter);
}
else
return prefix.toString();
}
return prefix.toString();
}
}
|
Complexity Analysis
1
2
3
4
5
6
7
| In the worst case query q has length m and is equal to all n strings of the array
Time Complexity: O(S) where S is the number of all characters in the array, LCP query O(m)
Trie build has O(S) time complexity. To find the common prefix of q
in the Trie takes in the worst O(m).
Space complexity: O(S) we only used additional S extra space for the Trie.
|
15-3Sum#
Given an array “nums” of n integers, are there elements a, b, c in nums such that a+b+c=0? Find all
unique triplets in the array which gives the sum of zero.
Note:
The solution set must not contain duplicate triplets
1
2
3
4
5
6
7
8
9
| Example:
Given array nums = [-1, 0, 1, 2, -1, -4].
A solution set is:
[
[-1, 0, 1],
[-1, -1, 2]
]
|
Sorted Array#
The method is to sort an input array and then run through all indices of a possible first element of a
triplet. For each element we make another 2Sum sweep of the remaining part of the array. Also we want
to skip elements to avoid duplicates in the answer without expending extra memory.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| public List<List<Integer>> threeSum(int[] num) {
//Arrays.sort re-arranges the array of integers in ascending order
//ex. [1, 2, 3, 4]
Arrays.sort(num);
List<List<Integer>> res = new LinkedList<>();
for (int i = 0; i < num.length-2; i++) {
if (i == 0 || (i > 0 && num[i] != num[i-1])) {
//This lets us skip some of the duplicate entries in the array
int lo = i+1, hi = num.length-1, sum = 0 - num[i];
//This is for the 2 Sum sweep
while (lo < hi) {
if (num[lo] + num[hi] == sum) {
res.add(Arrays.asList(num[i], num[lo], num[hi]));
while (lo < hi && num[lo] == num[lo+1]) lo++;
while (lo < hi && num[hi] == num[hi-1]) hi--;
//This lets us skip some of the duplicate entries in the array
lo++; hi--;
} else if (num[lo] + num[hi] < sum) lo++;
else hi--;
//This allows us to optimize slightly since we know that the array is sorted
}
}
}
return res;
}
|
Complexity Analysis
1
2
3
4
5
6
| Time Complexity: O(n^2) We go through a maximum of n elements for the first element of a triplet,
and then when making a bi-directional 2Sum sweep of the remaining part of
the array we also go through a maxiumum of n elements.
Space Complexity: O(1) If we assume the return linked list is not extra space, then we do not
allocate any significant extra space
|
16-3Sum Closest#
Given an array nums of n integers and an integer target, find three integers in nums such that the sum
is closest to target. Return the sum of the three integers. You may assume that each input would have
exactly one solution.
1
2
3
4
5
| Example:
Given array nums=[-1, 2, 1, -4], and target=1.
The sum that is closest to the target is 2. (-1+2+1=2)
|
3 Pointers#
Similar to the previous 3Sum problem, we use three pointers to point to the current element, next
element and the last element. If the sum is less than the target, it means that we need to add a larger
element so next element move to the next. If the sum is greater, it means we have to add a smaller
element so last element move to the second last element. Keep doing this until the end. Each time
compare the difference between sum and target, if it is less than minimum difference so far, then
replace result with it, otherwise continue iterating.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public class Solution {
public int threeSumClosest(int[] num, int target) {
int result=num[0] + num[1] + num[num.length-1];
Arrays.sort(num);
for (int i=0; i<num.length -2; i++) {
int start= i+1, end = num.length -1;
while (start < end) {
int sum = num[i] + num[start] + num[end];
if (sum > target) {
end--;
} else {
start++;
}
if (Math.abs(sum-target) < Math.abs(result-target)) {
result=sum;
}
}
}
return result;
}
}
|
17-Letter Combinations of a Phone Number#
Given a string contianing digits from 2-9 inclusive, return all possible letter combinations that the
number could represent.
A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not
map to any letters.
1
2
3
| 2 - abc 3 - def 4 - ghi 5 - jkl 6 - mno 7 - pqrs 8 - tuv
9 - wxyz
|
1
2
3
4
5
6
| Example:
Input: "23"
Output: ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
|
Note: The above answer is in lexicographical order but the answer can be in any order
Backtracking#
Backtracking is an algorithm for finding all solutions by exploring all potential candidates. If the
solution candidate turns to not be a solution (or at least not the last one), backtracking algorithm
discards it by making some changes on the previous step, ie backtracks and then tries again.
Here is a backtrack function backtrack(combination, next_digits) which takes as arguments an ongoing
letter combination and the next digits to check.
- If there are no more digits to check that means the current combination is done
- If there are still digits to check:
- Iterate over the letters mapping to the next available digit
- Append the current letter to the current combination and proceed to check next digits:
1
2
3
| combination = combination + letter
backtrack(combination + letter, next_digits[1:]).
|
Visual Representation

Complexity Analysis
1
2
3
4
5
6
7
|
Time Complexity: O(3^N * 4^M) where N is the number of digits in the input that maps to 3
letters (eg. 2, 3, 4, 5, 6, 8) and M is the number of digits
in the input that maps to 4 letters (eg. 7, 9) and N+M is the
total number digits in the input
Space Complexity: O(3^N * 4^M) since one has to keep 3^N * 4^M solutions
|
First In First Out (FIFO) Queue#
This solution utilizes the Single Queue Breadth First Search (BFS) which is an algorithm for traversing
or searching tree or graph data structures. It starts at the tree root and explores all of the neighbor
nodes.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public List<String> letterCombinations(String digits) {
LinkedList<String> ans = new LinkedList<String>();
if (digits.isEmpty()) return ans;
String[] mapping = new String[] {"0", "1", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", {wxyz"};
ans.add("");
for (int i = 0; i<digits.length(); i++) {
int x = Character.getNumericValue(digits.charAt(i));
//we terminate the while loop when we encounter a new-formed string which is more than
//the current level i
//peek retrieves the first value of the linked list
while (ans.peek().length==i){
//removes the head or the first value in the linkedlist
String t = ans.remove();
for (char s : mapping[x].toCharArray()) {
ans.add(t+s);
//this works because add appends to the end of the list
}
}
return ans;
}
}
|
Complexity Analysis
1
2
3
4
5
6
7
|
Time Complexity: O(3^N * 4^M) where N is the number of digits in the input that maps to 3
letters (eg. 2, 3, 4, 5, 6, 8) and M is the number of digits
in the input that maps to 4 letters (eg. 7, 9) and N+M is the
total number digits in the input
Space Complexity: O(3^N * 4^M) since one has to keep 3^N * 4^M solutions
|
18-4Sum#
Given an array nums of n integers and an integer target, are there elements a, b, c, and d in nums such
that a + b + c + d = target? Find all unique quadruplets in the array which gives the sum of target
Note:
The solution set must not contain duplicate quadruplets
1
2
3
4
5
6
7
8
9
10
11
12
13
| Example:
Given array nums = [1, 0, -1, 0, -2, 2], and target = 0
A solution set is:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]
|
Sorted Array#
The idea is the same as the other numbered sum problems like 2sum and 3sum. We sort the array and then
proceed to interate through the values until we end up with a result that we are looking for.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
| public class Solution {
public List<List<Integer>> fourSum(int[] num, int target) {
ArrayList<List<Integer>> ans = new ArrayList<>();
if (num.length<4) {
return ans;
}
Arrays.sort(num);
for (int i=0; i<num.length-3; i++) { //picking the first candidate must leave room
//for the other values
if (num[i]+num[i+1]+num[i+2]+num[i+3]>target) {
break;
//first candidate too large, search finished
}
if (num[i]+num[num.length-1]+num[num.length-2]+num[num.length-3]<target) {
continue;
//first candidate too small
}
if(i>0 && num[i]==num[i-1]) {
continue;
//prevents duplicate in ans list
}
for (int j=i+1; j<num.length-2; j++) { //picking the second candidate must
//leave room for other values
if (num[i]+num[j]+num[j+1]+num[j+2]>target) {
break;
//second candidate too large
}
if (num[i]+num[j]+num[num.length-1]+num[num.length-2]<target) {
continue;
//second candidate too small
}
if(j>i+1 && num[j]==num[j-1]) {
continue;
//prevents duplicate results in ans list
}
int low=j+1, high=num.length-1;
//two pointer search
while(low<high) {
int sum=num[i]+num[j]+num[low]+num[high];
if (sum==target) {
ans.add(Arrays.asList(num[i],num[j],num[low],num[high]));
while(low<high&&num[low]==num[low+1]) {
low++; //skipping over duplicates
}
while(low<high && num[high]==num[high-1] {
high--; //skipping over duplicates
}
low++;
high--;
}
//moving window
else if (sum<target) {
low++;
}
else {
high--;
}
}
}
}
return ans;
}
}
|
19-Remove Nth Node From End of List#
Given a linked list, remove the n-th node from the end of the list and return its head
1
2
3
4
5
6
7
8
| Example:
Given linked list: 1 -> 2 -> 3 -> 4 -> 5, and n=2
After removing the second node from the end, the linked list becomes
1 -> 2 -> 3 -> 5
|
Note:
Given n will always be valid
Follow up:
Could you do this in one pass?
Two Pass Algorithm#
Intuition
We notice that the problem could be simply reduced to another one: Remove the (L-n+1)th node from the
beginning of the list, where L is the list length. This problem is easy to solve once we found the
list length L.
Algorithm
First we will add an auxiliary “dummy” node, which points to the list head. The “dummy” node is used to
simplify some corner cases such as a list with only one node or removing the head of the list. On the
first pass, find the list length L. Then we set a pointer to the dummy node and start to move it
through the list till it comes to the (L-n)th node. We relink next pointer of the (L-n)th node to the
(L-n+2)th node and we are done.
1
2
3
4
5
6
| D -> 1 -> 2 -> 3 -> 4 -> NULL
|
v
D -> 1 -> 2 -> 4 -> NULL
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0);
dummy.next = head;
int length =0;
ListNode first = head;
while (first!=null) {
length++;
first=first.next;
}
length -= n;
first = dummy;
while (length>0) {
length--;
first=first.next;
}
first.next=first.next.next;
return dummy.next;
}
|
Complexity Analysis
1
2
3
4
5
| Time Complexity: O(L) The algorithm makes two traversals of the list, first to calculate the
list length L and second to find the (L-n)th node. There are 2L-n
operations and time complexity is O(L)
Space Complexity: O(1) We only used constant extra space
|
One Pass Algorithm#
The previous algorithm could be optimized to one pass. Instead of one pointer, we could use two
pointers. The first pointer advances the list by n+1 steps from the beginning, while the second pointer
starts from the beginning of the list. Now, both pointers are separated by exactly n nodes. We maintain
this constant gap by advancing both pointers together until the first pointer arrives past the last
node. The second pointer will be pointing at the nth node counting from the last. We relink the next
pointer of the node referenced by the second pointer to point to the node’s next next node.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| Maintaining N=2 nodes apart between the first and second pointer
D -> 1 -> 2 -> 3 -> 4 -> 5 -> NULL
first Head
second
Move the first pointer N+1 steps
|
v
D -> 1 -> 2 -> 3 -> 4 -> 5 -> NULL
second Head First
Move the first and second pointers together until the first pointer arrives past the last node
|
v
D -> 1 -> 2 -> 3 -> 4 -> 5 -> NULL
Head Second First
Second pointer points to the nth node counting from last so link node to the node's next next node
|
v
D -> 1 -> 2 -> 3 -> -> 5 -> NULL
Head Second First
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode first = dummy;
ListNode second = dummy;
//Moves the first pointer so that the first and second nodes are separated by n nodes
for (int i=1; i<=n+1; i++) {
first = first.next;
}
//Move first to the end, maintaining the gap
while (first!=null) {
first=first.next;
second=second.next;
}
second.next=second.next.next;
return dummy.next;
}
|
Complexity Analysis
1
2
3
4
| Time Complexity: O(L) The algorithm makes one traversal of the list of L nodes. Therefore
time complexity is O(L)
Space Complexity: O(1) Only constant extra space was used
|
20-Valid Parentheses#
Given a string containing just the characters ‘(’, ‘)’, ‘{’, ‘}’, ‘[’, ‘]’, determine if the input
string is valid
An input string is valid if:
- Open brackets must be closed by the same type of brackets
- Open brackets must be closed in the correct order
Note that an empty string is also considered valid
1
2
3
4
| Example 1:
Input: "()"
Output: true
|
1
2
3
4
| Example 2:
Input: "()[]{}"
Output: true
|
1
2
3
4
| Example 3:
Input: "(]"
Output: false
|
1
2
3
4
| Example 4:
Input: "([)]"
Output: false
|
1
2
3
4
| Example 5:
Input: "{[]}"
Output: true
|
Counting method#
Intuition
Imagine you are writing a small compiler for your college project and one of the tasks or sub-tasks for
the compiler would be to detect if the parenthesis are in place or not.
The algorithm we will look at in this article can be then used to process all the parenthesis in the
program your compiler is compiling and checking if all the parenthesis are in place. This makes
checking if a given string of parenthesis is valid or not, an important programming problem.
The expressions that we will deal with in this problem can consist of three different types of
parenthesis:
Before looking at how we can check if a given expression consisting of thes parenthesis is valid or
not, let us look at a simpler version of the problem that consists of just one type of parenthesis. So,
the expressions we can encounter in this simplified version of the problem are:
1
2
3
4
5
6
7
| (((((()))))) -- VALID
()()()() -- VALID
(((((((() -- INVALID
((()(()))) -- VALID
|
Let’s look at a simple algorithm to deal with this problem
We process the expression one bracket at a time starting from the left
Suppose we encounter an opening bracket ie. (, it may or may not be an invalid expression because
there can be a matching ending bracket somewhere in the remaining part of the expression. Here, we
simply increment the counter keeping track of the left parenthesis till now. left += 1
If we encounter a closing bracket, this has two meanings:
There was no matching opening bracket for this closing bracket and in that case we have an invalid
expression. This is the case when left==0 ie. when there are no unmatched left brackets
available
We had some unmatched opening bracket available to match this closing bracket. This is the case
when left>0 ie. we have unmatched left brackets available
If we encounter a closing bracket ie. ) when left==0, then we have an invalid expression on our
hands. Else, we decrement left thus reducing the number of unmatched left parenthesis available.
Continue processing the string until all parenthesis have been processed
If in the end we still have an unmatched left parenthesis available, this implies an invalid
expression
The reason we discussed this particular algorithm here is because the approach for the approach for
the original problem derives its inspiration from this very solution.
If we try and follow the same approach for our original problem, then it simply won’t work. The reason
a simple counter based approach works above is because all the parenthesis are of the same type. So
when we encounter a closing bracket, we simply assume a corresponding opening matching bracket
to be available ie. if left>0
But in our problem, if we encounter say ], we don’t really know if there is a corresponding opening
[ available or not. You could say:
Why not maintain a separate counter for the different types of parenthesis?
This doesn’t work because the relative placement of the parenthesis also matters here eg: [{]
If we simply keep counters here, then as soon as we encounter the closing square bracket, we would
know there is an unmatched opening square bracket available as well. But, the **closest unmatched
opening bracket available is a curly bracket and not a square bracket and hence the counting approach
breaks here.
Stacks#
An interesting property about a valid parenthesis expression is that a sub-expression. (Not every
sub-expression) eg.
1
2
3
4
| { [ [ ] { } ] } ( ) ( )
^ ^
| |
|
The entire expression is valid, but sub portions of it are also valid in themselves. This lends a sort
of a recursive structure to the problem. For example consider the expression enclosed within the
marked parenthesis in the diagram above. The opening bracket is at index 1 and the corresponding
closing bracket is at index 6.
What if whenever we encounter a matching pair of parenthesis in the expression we simply remove it
from the expression?
Let’s have a look at this idea below where we remove the smaller expressions one at a time from the
overall expression and since this is a valid expression, we would be left with an empty string in the
end.
1
2
3
| The stack data structure can come in handy here in representing this recursive structure of the
problem. We can't really process this from the inside out because we don't have an idea about the
overall structure. But, the stack can help us process this recursively ie. from outside to inwards.
|
Lets take a look at the algorithm for this problem using stacks as the intermediate data structure.
Algorithm
- Initialize a stack S.
- Process each bracket of the expression one at a time
- If we encounter an opening bracket, we simply push it onto the stack. This means we will process it
later, let us simply move onto the sub-expression ahead
- If encounter a closing bracket, then we check the element on top of the stack. If the element at the
top of the stack is an opening bracket
of the same type, then we pop it off the stack and continue
processing. Else, this implies an invalid expression - In the end, if we are left with a stack still having elements, then this implies an invalid
expression
Lets take a look at the implementation for this algorithm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| class Solution {
//Hash table that takes care of the mappings
private HashMap<Character, Character> mappings;
//Initialize the hash map with mappings. This simply makes the code easier to read
public Solution() {
this.mappings = new HashMap<Character, Character>();
this.mappings.put(')', '(');
this.mappings.put('}', '{');
this.mappings.put(']', '[');
}
public boolean isValid(String s) {
// Initialize a stack to be used in the algorithm
Stack<Character> stack = new Stack<Character>();
for (int i=0; i< s.length(); i++) {
char c = s.charAt(i);
// If the current character is a closing bracket
if (this.mappings.containsKey(c)) {
// Get the top element of the stack. If the stack is empty, set a dummy value of '#'
char topElement = stack.empty() ? '#' : stack.pop();
// If the mapping for this bracket doesn't match the stack's top element, return false.
if (topElement != this.mappings.get(c)) {
return false;
}
} else {
//If it was an opening bracket, push to the stack
stack.push(c);
}
}
//If the stack still contains elements, then it is an invalid expression.
return stack.isEmpty();
}
}
|
Complexity Analysis
1
2
3
4
5
| Time Complexity: O(n) We simply traverse the given string one character at a time and push
and pop operations on a stack take O(1) time
Space Complexity: O(n) In the worst case, when we push all opening brackets onto the stack, we
will end up pushing all the brackets onto the stack eg (((((((((((
|
21-Merge Two Sorted Lists#
Merge two sorted linked lists and return it as a new list. The new list should be made by splicing
together the nodes of the first two lists.
1
2
3
4
| Example:
Input: 1->2->4, 1->3->4
Output: 1->1->2->3->4->4
|
Recursive#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if (l1 == null) return l2;
if (l2 == null) return l1;
if (l1.val < l2.val) {
l1.next = mergeTwoLists(l1.next, l2);
return l1;
} else {
l2.next = mergeTwoLists(l1, l2.next);
return l2;
}
}
}
|
Non-Recursive#
Similar approach and implemenation to the recursive solution above but a little more intuitive and
does not require memory being held on the stack (as the recursive program runs it has to store
variables on the stack so that when the program jumps back it is able to continue)
As with most other linked list solutions, a dummy node is utilized and two pointers are used to keep
track of where we are in the the two linked lists.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode returnNode = new ListNode(-1);
ListNode headNode = returnNode;
while (l1 != null && l2 != null) {
if (l1.val <= l2.val) {
returnNode.next = l1;
l1 = l1.next;
} else {
returnNode.next = l2;
l2 = l2.next;
}
returnNode = returnNode.next;
}
if (l1 == null) {
returnNode.next = l2;
} else if (l2 == null) {
returnNode.next = l1;
}
return headNode.next;
}
}
|
22-Generate Parentheses#
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
1
2
3
4
5
6
7
8
9
10
11
| For example:
Given n=3, a solution set is:
[
"((()))",
"(()())".
"(())()",
"()(())",
"()()()"
]
|
Brute Force#
Intuition
We can generate all 2^(2n) sequences of ( and ) characters. Then we can check if each one is valid
Algorithm
To generate all sequences, we use recursion. All sequences of length n is just ( plus all sequences
of length n-1, and then ) plus all sequences of length n-1.
To check whether a sequence is valid, we keep track of balance, the net number of opening brackets
minuts closing brackets. If it falls below zero at any time, or doesn’t end in zero, the sequence is
invalid - otherwise it is valid.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Solution {
public List<String> generateParenthesis(int n) {
List<String> combinations = new ArrayList();
generateAll(new char[2*n], 0, combinations);
return combinations;
}
public void generateAll(char[] current, int pos, List<String> result) {
if(pos == current.length) {
if (valid(current)) {
result.add(new String(current));
}
} else {
current[pos] = '(';
generateAll(current, pos+1, result);
current[pos] = ')';
generateAll(current, pos+1, result);
}
}
public boolean valid(char[] current) {
int balance = 0;
for (char c : current) {
if(c == '(') {
balance++;
} else {
balance--;
}
if(balance < 0) {
return false;
}
}
return (balance == 0);
}
}
|
Complexity Analysis
1
2
3
4
5
| Time Complexity: O(2^2n * n) For each of 2^2n sequences, we need to create an validate the
sequence, which takes O(n) work in the worst case
Space Complexity: O(2^2n * n) Naively, every sequence could be valid, see Closure number for
a tighter asymptotic bound
|
Backtracking#
Intuition and Algorithm
Instead of adding ( or ) every time as we do in the Brute Force algorithm, let’s only add them
when we know it will remain a valid sequence. We can do this by keeping track of the number of opening
and closing brackets we have placed so far.
We can start an opening bracket if we still have one (of n) left to place. And we can start a closing
bracket if it would not exceed the number of opening brackets
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public List<String> generateParenthesis(int n) {
List<String> ans = new ArrayList();
backtrack(ans, "", 0, 0, n);
return ans;
}
public void backtrack(List<String> ans, String cur, int open, int close, int max){
if (cur.length() == max*2) {
ans.add(cur);
return;
}
if(open < max) {
backtrack(ans, cur + "(", open + 1, close, max);
}
if (close < open) {
backtrack(ans, cur + ")", open, close +1, max);
}
}
}
|
Complexity Analysis
Our complexity analysis rests on understanding how many elements there are in generateParenthesis(n).
This analysis is outside the scope of this article, but it turns out this is the nth Catalan number
1/(n+1) (2n choose n), which is bounded asymptotically by 4^n/(n* sqrt(n)).
1
2
3
4
5
| Time Complexity: O((4^n)/sqrt(n)) Each valid sequence has at most n steps during the
backtracking procedure
Space Complexity: O((4^n)/sqrt(n)) As described above and using O(n) space to store the
sequence
|
Another way to think about the runtime of backtracking algorithms on interviewers is O(b^d), where b is
the branching factor and d is the maximum depth of recursion.
Backtracking is characterized by a number of decisions b that can be made at each level of recursion.
If you visualize the recursion tree, this is the number of children each internal node has. You can
also think of b as standing for “base”, which helps us remember that b is the base of the exponential.
If we make b decisions at each level of recursion, and we expand the recursion tree to d levels (ie.
each path has a length of d), then we get b^d nodes. Since backtracking is exhaustive and must visit
each of these nodes, the runtime is O(b^d)
Closure Number#
To enumerate something, generally we would like to express it as a sum of disjoint subsets that are
easier to count.
Consider the closure number of a valid parentheses sequence s: the least index >= 0 so that
`S[0], S[1], … , S[2 * index + 1] is valid. Clearly, every parentheses sequence has a unique closure
number. We can try to enumerate them individually.
Algorithm
For each closure number c, we know the starting and ending brackets must be at index 0 and
2 * c + 1. Then, the 2 * c elements between must be a valid sequence, plus the rest of the elements
must be a valid sequence.
This is just some minor improvement to the backtracking solution using the fact that for all valid
solutions the first char is always ‘(’ and the lat char is always ‘)’. We initialize the starting
string to ‘(’ and set the recursion bottom condition to string reaching length of 2 * n - 1 - we know
that we need to append a bracket at the end. There will not be much of an improvement in the runtime
however.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public List<String> generateParenthesis(int n) {
List<String> ans = new ArrayList();
if (n==0) {
ans.add("");
} else {
for (int c=0; c<n; ++c)
for (String left: generateParenthesis(c))
for (String right: generateParenthesis(n-1-c))
ans.add("(" + left + ")" + right);
}
return ans;
}
}
|
Complexity Analysis
1
2
3
| Time Complexity: O((4^n)/sqrt(n))
Space Complexity: O((4^n)/sqrt(n))
|
23-Merge k Sorted Lists#
Merge k sorted linked lists and return it as one sorted list. Analyze and descibe its complexity:
1
2
3
4
5
6
7
8
9
10
| Example:
Input:
[
1 -> 4 -> 5,
1 -> 3 -> 4,
2 -> 6
]
Output: 1 -> 1 -> 2 -> 3 -> 4 -> 4 -> 5 -> 6
|
Brute Force#
Intuition and Algorithm
- Traverse all the linked lists and collect the values of the nodes into an array
- Sort and iterate over this array to get the proper value of nodes
- Create a new sorted linked list and extend it with the new nodes
As for sorting you can refer to the Algorithms/Data Structures CheatSheet for more about sorting algorithms.
146-LRU Cache#
Design and implement a data structure for Least Recently Used (LRU) cache. It should support the following operations: get and put.
get(key) - Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1
put(key, value) - Set or insert the value if the key is not already present. When the cache reached its capacity, it should invalidate the least recently used item before inserting a new item.
Follow up:
Could both of these operations be done in O(1) time complexity?
Example:
1
2
3
4
5
6
7
8
| LRUCache cache = new LRUCache(2 /* capacity */);
cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // returns 1
cache.put(3, 3); // evicts key 2
cache.get(2); // returns -1 (not found)
|
1
2
3
4
5
6
7
8
9
10
11
12
| public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
TreeNode current = root;
while (current != null){
if (p.val < current.val && q.val < current.val) // Both located in left side.
current = current.left;
else if (p.val > current.val && q.val > current.val) // Both located in right side
current = current.right;
else
return current; // Seperate branches, therefore current is lca.
}
return null;
}
|
The updated version runs in 2ms and passes 96.85% submissions.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public String countAndSay(int n) {
String result = "1"; // initial result
StringBuilder temp; // to create intermediate strings efficiently.
int len; // length of the result string.
for (int i = 1; i < n; ++i){ // We need to iterate n-1 times, because 1st result is 1
int startIndex = 0; // we will look at each index of result
temp = new StringBuilder(); // and store freq,char in the builder
len = result.length();
while (startIndex < len){
char ch = result.charAt(startIndex++); // get the char at startIndex, and increment it, because we also want to look at the next character
int count = 1; // intialize it's count to 1, we just saw it.
while (startIndex < len && ch == result.charAt(startIndex)){
count++; // If next also matches, increment count and startIndex
startIndex++;
}
temp.append(count).append(ch); // No more match, Add the freq and the char
}
result = temp.toString(); // Update result to generate the next cound-and-say
}
return result;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public int maxSubArray(int[] nums) {
int localMax = nums[0]; // keeps track of max sum between the previous and current
int globalMax = nums[0]; // keeps track of global max sum.
/*
The idea is as follows:
If the current element is greater than the previous local max, then we found an element that is a better option then before.
Then, if that localmax changed and is greater than our global max, update our global max.
*/
for (int i = 1; i < nums.length; i++){
localMax = Math.max(localMax + nums[i], nums[i]);
globalMax = Math.max(localMax, globalMax);
}
return globalMax;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public int[] plusOne(int[] digits)
{
digits[digits.length-1]++; // Add one to the last place.
if (digits[digits.length-1] == 10) // If it became 10,
{
for (int i = digits.length-1; i > 0; i--) // Then add one to its previous place
{
if (digits[i] == 10){ // If that also results in 10, keep propogating that 1
digits[i-1]++; // upstream
digits[i] = 0;
}
}
if (digits[0] == 10){ // If the index 0 is 10, then the number is a multiple of 10.
digits = new int[digits.length+1];
digits[0] = 1; // So increase length by 1 and set index 0 to 1.
}
}
return digits;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| public int mySqrt(int x) {
long x1 = 10 - (100 - x)/20; // Using Newton's method of computing square roots.
boolean done = false;
while (!done)
{
long x2 = x1 - (x1*x1 - x)/(2*x1);
if (x2 == x1)
done = true;
else
x1 = x2;
}
return (int)x1-1;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| public int climbStairs(int n) {
if (n < 4) // I chose n < 4 because climbStairs(0 <= n <= 3) = n
return n;
int[] dp = new int[n+1];
for (int i = 0; i < 4; i++)
dp[i] = i;
//return naiveDP(n, dp);
return efficientDP(n);
}
public int naiveDP(int n, int dp[]){
if (dp[n] != 0) // If already computed, return it.
return dp[n];
int ways = naiveDP(n-1, dp) + naiveDP(n-2, dp); // Just like Fibonacci.
dp[n] = ways; // Save it.
return ways;
}
public int efficientDP(int n){
if (n < 4)
return n;
int[] dp = new int[n+1]; // Initialize dp of length n+1 to store n'th way.
for (int i = 0; i < 4; i++)
dp[i] = i; // climbStairs(0 <= n <= 3) = n
for (int i = 3; i <= n; i++) // climbStairs(n) = climbStairs(n-1) + climbstairs(n-2);
dp[i] = dp[i-1] + dp[i-2]; // So fetch those values from the dp array.
return dp[n];
}
|
1
2
3
4
5
6
7
8
9
10
11
12
| public ListNode deleteDuplicates(ListNode head){
ListNode current = head;
// while we haven't reached the tail
while (current != null && current.next != null)
{
// if current's next is the same as current, skip and update its next
while (current.next != null && current.val == current.next.val)
current.next = current.next.next;
current = current.next;
}
return head;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
| public boolean isSameTree(TreeNode p, TreeNode q)
{
if (p == null && q == null) // Two empty trees
return true;
// If one of the node is null, the two trees can't be equal.
if ((p == null && q != null) || (p != null && q == null))
return false;
// If the values in the two nodes are same, compare its's left and right sub-tree.
if (p.val == q.val)
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
return false; // If nothing worked out, they can't be same.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| public boolean isSymmetric(TreeNode root)
{
return isSymmetricIterative(root);
}
public boolean isSymmetricIterative(TreeNode root)
{
Queue<TreeNode> track = new LinkedList<>();
track.add(root); // Add the root twice so we can compare its left and right
track.add(root);
while (!track.isEmpty())
{
TreeNode x = track.poll(); // Remove 2 nodes
TreeNode y = track.poll();
if (x == null && y == null) // If they are both null, skip it.
continue;
if (x == null || y == null || x.val != y.val)
return false; // If values don't match or one is null
track.add(x.left); // Otherwise add them in this order -> LRRL
track.add(y.right); // because we need to compare left most with the
track.add(x.right); // right most, then inner left with inner right.
track.add(y.left);
}
return true; // Everything's all right, so they must be symmetric.
}
public boolean isSymmetricRecursive(TreeNode root)
{
return helperRecursive(root, root);
}
private boolean helperRecursive(TreeNode x, TreeNode y)
{
if (x == null || y == null) // Base Case: Both or one is null, so true
return true;
return (x.val == y.val && helperRecursive(x.left, y.right) && helperRecursive(x.right, y.left));
// Check if values match and 1.left matches with the 2.right and 1.right matches with 2.left
}
|
1
2
3
4
5
6
| /*
If root is null, height is 0 else add 1 and find if the left or the right has a greater depth.
*/
public int maxDepth(TreeNode root) {
return root == null ? 0 : 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public TreeNode sortedArrayToBST(int[] nums)
{
return aux(nums, 0, nums.length-1);
}
private TreeNode aux(int[] n, int left, int right)
{
if (left > right) // Either empty, or return a null node
return null;
int mid = (left+right+1)/2; // Create a node with the middle value
TreeNode root = new TreeNode(n[mid]);
root.left = aux(n, left, mid-1); // Compute the left (which is the mid in left side)
root.right = aux(n, mid+1, right); // Compute the right (which is the mid in right side)
return root;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| public boolean isBalanced(TreeNode root)
{
return isBalancedBottomUp(root);
}
public boolean isBalancedTopDown(TreeNode root)
{
if (root == null)
return true;
// if difference between root's left and right is > 1, they're not balanced
if (Math.abs((getHeight(root.left) - getHeight(root.right))) > 1)
return false;
// otherwise, we need to check if the left and right subtree are also balanced.
return isBalanced(root.left) && isBalanced(root.right);
}
private int getHeight(TreeNode node)
{
// Standard height of a binary tree calculator
if (node == null)
return 0;
return 1 + Math.max(getHeight(node.left), getHeight(node.right));
}
public boolean isBalancedBottomUp(TreeNode root)
{
return getHeight2(root) != -1; // -1 means not balanced.
}
private int getHeight2(TreeNode node)
{
if (node == null)
return 0;
int lHeight = getHeight2(node.left); // Get the height of left and right tree
int rHeight = getHeight2(node.right);
// If at any point there was a height difference of more than 1 or previous node's leftheight || rightheight returned -1, return -1 to let the next node know there was an imbalance.
if ((Math.abs(lHeight-rHeight) > 1) || lHeight == -1 || rHeight == -1)
return -1;
return 1 + Math.max(lHeight, rHeight); // Else carry on with the normal procedure
}
|
1
2
3
4
5
6
7
8
9
10
| public int minDepth(TreeNode root) {
// Base case
if (root == null) return 0;
// Left is null, find minheight from right side
if (root.left == null) return 1 + minDepth(root.right);
// Right is null, find minheight from left side
if (root.right == null) return 1 + minDepth(root.left);
// Else, both are not null, so compute min height from the two sides.
return 1 + Math.min(minDepth(root.left), minDepth(root.right));
}
|
1
2
3
4
5
6
7
8
9
| public boolean hasPathSum(TreeNode root, int sum) {
if (root == null)
return false; // No sum exist
sum -= root.val; // Sum decreases
if (root.left == null && root.right == null) // If we are at a leaf
return sum == 0; // Check if the sum is 0.
return hasPathSum(root.left, sum) || hasPathSum(root.right, sum);
// Otherwise look if you can make sum = 0 by exploring the left or right side.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public List<List<Integer>> generate(int numRows) {
List<List<Integer>> pt = new ArrayList<>();
for (int i = 0; i < numRows; i++) // Need to add all n rows
{
List<Integer> temp = new ArrayList<>(); // temp list to store values
for (int j = 0; j <= i; j++)
{
if (j == 0 || i == j) // First and last values are always 1.
temp.add(1);
else // Else, get the previous row and surrounding two values and add them
temp.add(pt.get(i-1).get(j-1) + pt.get(i-1).get(j));
}
pt.add(temp); // Add it to pt.
}
return pt;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public boolean isPalindrome(String s) {
if (s.length() > 0){ // Only do this is s is not empty
s = s.toLowerCase(); // Convert it to lowercase
int left = 0; // Initialize left and right pointers
int right = s.length()-1;
while (left < right) // continue while we haven't hit the middle of the string
{
// If char at left is not a letter or a number, skip it.
if (!Character.isLetter(s.charAt(left)) && !Character.isDigit(s.charAt(left)))
left++;
// Same with char at right.
else if (!Character.isLetter(s.charAt(right)) && !Character.isDigit(s.charAt(right)))
right--;
//Char's are now alphanumeric.
else if (s.charAt(left) != s.charAt(right)) // If they don't match
return false; // return false
else // They matched, so try to match the inner string
{
left++;
right--;
}
}
}
return true; // No mismatch found, return true.
}
|
1
2
3
4
5
6
7
8
9
| public List<Integer> getRow(int rowIndex)
{
ArrayList<Integer> row = new ArrayList<>();
row.add(1); // First is always 1.
// Using the nth row formula to compute the coeeficients. You can google "nth row Pascal"
for (int i = 0; i < rowIndex; i++)
row.add((int)(1.0*row.get(i)*(rowIndex-i)/(i+1)));
return row;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| /*
The general idea is that if the price you are looking at right now in the array minus the minimum observed so far is greater than the maximum profit you recorded, update the max.
*/
public int maxProfit(int[] prices) {
if (prices.length == 0) // Empty array
return 0;
int min = prices[0];
int max = 0;
for (int i = 1; i < prices.length; i++)
{
if (prices[i] < min)
min = prices[i];
else if (prices[i] - min > max)
max = prices[i]-min;
}
return max;
}
|
1
2
3
4
5
6
7
8
9
10
| /*
The general idea is that the moment you observe a valley and consecutive peak, make the trade by buying the stock on the valley day and selling it on the peak day.
*/
public int maxProfit(int[] prices) {
int sum = 0;
for (int i = 0; i < prices.length-1; i++)
if (prices[i+1] > prices[i])
sum += (prices[i+1] - prices[i]);
return sum;
}
|
1
2
3
4
5
6
7
8
9
| /*
The general idea is that XOR of two same numbers returns 0 and XOR with 0 returns the same number. So if there is only one element that doesn't have a pair, all the remaining will XOR with themselves at one point and give 0 but not the singleton element.
*/
public int singleNumber(int[] nums) {
int num = nums[0];
for (int i = 1; i < nums.length; i++)
num ^= nums[i];
return num;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| // Using the slow-fast runner technique.
public boolean hasCycle(ListNode head) {
if (head == null)
return false;
ListNode first = head; // Slow runner
ListNode second = first.next; // Fast Runner
// while second is not at the end or it isn't the tail
while (second != null && second.next != null)
{
if (second == first) // If fast made a full loop and met up with slow
return true; // We got a cycle
first = first.next; // Slow moves one step
second = second.next.next; // Second advances two.
}
return false; // We don't have a cycle
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class MinStack {
int min;
Stack<Integer> stack;
public MinStack() {
min = Integer.MAX_VALUE;
stack = new Stack<>();
}
public void push(int x) {
stack.push(x); // Push the value
if (x < min) // If that value is minimum than we have, update min
min = x;
stack.push(min); // Push the minimum on top of the stack for constant time
} // minimum retrieval.
public void pop() {
stack.pop(); // Pop the minimum.
stack.pop(); // Pop the actual element meant to be popped
if (stack.isEmpty()) // If empty, min is Max int value
min = Integer.MAX_VALUE;
else
min = stack.peek(); // Otherwise, min would be the top most element since we
} // always push the minimum on top of any element we push.
public int top() {
return stack.elementAt(stack.size()-2); // Top element is actually at second last
} // index since the last element is the minimum.
public int getMin() {
return min;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| /*
The general idea is that if you are done traversing any of the lists, make it's pointer point to the head of the other list and start iterating. The reasoning is that the second time they iterate, they will have traversed exactly the same distance (it's length plus the other list's head to the intersecting node) and will meet at the intersecting node.
*/
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
int count = 0;
ListNode pA = headA;
ListNode pB = headB;
while (pA != pB){
pA = pA == null ? headB : pA.next;
pB = pB == null ? headA : pB.next;
}
return pA;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public int[] twoSum(int[] numbers, int target) {
int left = 0, right = numbers.length-1;
while (left < right) // Narrow down the window from both sides until they add up.
{
int sum = numbers[left] + numbers[right];
if (sum > target) // We overshot, so decrease the window from right
right--;
else if (sum < target) // Undershot, increase windows from left so next sum is more
left++;
else
break; // Found the two numbers
}
return new int[] {left+1, right+1}; // +1 because LeetCode followed 1-n indexing.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
| public String convertToTitle(int n) {
String res = "";
while (n > 0)
{
/* 1 is A and 26 is Z, so n-1 to change it to 0-25 scheme. Then, % 26 to find how
much it is off on a full alphabet cycle, add 65 (ASCII for A) and convert it to char
*/
res = String.valueOf((char)(65+((n-1)%26))) + res;
n = (n-1) / 26; // Subtract 1 and divide by 26 to get prepare for the next character
}
return res;
}
|
Uses Moore’s Algorithm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| // This is the implementation of Moore's Algorithm for O(n) complexity.
public int majorityElement(int[] nums) {
int major = nums[0];
int count = 1;
for (int i = 0; i < nums.length; i++){
if (major == nums[i])
count++;
else
count--;
if (count == 0){
major = nums[i];
count = 1;
}
}
return major;
}
|
1
2
3
4
5
6
7
8
9
10
| /*
Start from the end of String s, compute the ASCII for the char, +1 for 1-26 Alphabet-Scheme (hence -64 instead of -65) and multiply it to 26^{distance from the end of the string}
*/
public int titleToNumber(String s) {
int length = s.length()-1;
int total = 0;
for (int i = length; i > -1; i--)
total += (int)(s.charAt(i)-64) * Math.pow(26,length-i);
return total;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
| /*
The general idea is that every factorial that has 5 as a multiple also has 2 to multiply to 10. So if we can count the number of times we can divide n by 5, should gives us the number of trailing zeroes. O(log(n) base 5) complexity.
*/
public int trailingZeroes(int n) {
int res = 0;
while (n > 4)
{
res += n / 5;
n /= 5;
}
return res;
}
|
1
2
| select FirstName, LastName, City, State
from Person left join Address on Address.personId = person.personId;
|
1
2
3
| select max(salary) as SecondHighestSalary
from Employee
where salary not in (select max(salary) from employee);
|
1
2
3
| select emp.Name as Employee
from Employee emp, Employee man
where emp.managerId = man.Id and emp.salary > man.salary;
|
1
2
3
4
| select email
from person
group by (email)
having count(*) > 1;
|
1
2
3
| select name as Customers
from Customers
where customers.id not in (select customerId from orders);
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public void rotate(int[] nums, int k) {
k %= nums.length; // k == nums.length ? Then it's a full rotation and no change
if (k == 0)
return;
reverse(nums, 0 , nums.length-1); // First reverse the full array
reverse(nums, 0, k-1); // Then reverse element from index 0 to k-1
reverse(nums, k, nums.length-1); // Then reverse all elements from k to end of Array
}
// Reverse function that reverses the array from specified indices.
public void reverse(int[] nums, int start, int end)
{
while (start < end){
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end--;
}
}
|
1
2
3
| delete from Person
where Id not in (select min_id from
(select min(Id) as min_id from Person group by Email) as a)
|
1
2
3
| select w2.id
from weather w1, weather w2
where Datediff(w2.recorddate, w1.recorddate) = 1 and w2.temperature > w1.temperature;
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| public boolean hasGroupsSizeX(int[] deck) {
HashMap<Integer, Integer> freq = new HashMap<>();
for (int i = 0; i < deck.length; i++) // Record the frequencies
freq.put(deck[i],freq.getOrDefault(deck[i],0)+1);
/*
deck = [1,1,2,2,2,2,3,3,3,3,3,3]
number 1 has len of 2, number 2 has len of 4, number 3 has len of 6, they share a Greatest common divisor of 2, which means diving them into group of size X = 2, will be valid. Thus we just have to ensure each length (of a number) shares a Greatest Common Divisor that's >= 2.
*/
int hcf = 0;
for (int i: freq.keySet())
hcf = gcd(hcf, freq.get(i));
return hcf > 1;
}
private static int gcd(int x, int y)
{
int temp = 0;
while (y != 0){
temp = y;
y = x % y;
x = temp;
}
return x;
}
|
1
2
3
4
5
6
7
8
9
10
| public int reverse(int x) {
int sign = x < 0 ? -1 : 1;
x = x * sign; // Make x positive
long n = 0;
while (x > 0){
n = n * 10 + x % 10; // Start adding from the end.
x /= 10;
}
return (int)n == n ? (int)n*sign : 0; // Try converting to int from long, if no change,
} // Return n * sign, else 0 cause overflow.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
int carry = 0; // To record the carry
int sum = 0; // To record the total of two vals
ListNode dummy = new ListNode(0); // Dummy's next is the actual head
ListNode curr = dummy;
do{
if (l1 == null) // If one of the node is null, we set it to a
l1 = new ListNode(0); // dummy value of 0 so we can adjust for
if (l2 == null) // different length of the two lists.
l2 = new ListNode(0);
sum = l1.val + l2.val + carry; // Add the two vals and the carry.
carry = sum < 10 ? 0 : 1; // Record the carry for the next iteration
curr.next = new ListNode(sum % 10); // next node's value is sum % 10.
curr = curr.next; // advance current, l1 and l2.
l1 = l1.next;
l2 = l2.next;
} while(l1 != null || l2 != null);
if (carry == 1) // In the end, if carry is 1, it was from
curr.next = new ListNode(carry); // from adding last terms, so make next node 1
return dummy.next; // Return the actual head.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| public int lengthOfLongestSubstring(String s) {
if (s == null || s.length() == 0)
return 0;
int[] hash = new int[128]; // To store the occurence of characters
int maxLength = 0;
for (int i = 0, j = 0; j < s.length(); j++){
i = Math.max(hash[s.charAt(j)], i); // Check the most recent index of character.
maxLength = Math.max(maxLength, j-i+1); // That minus current pointer gives length
hash[s.charAt(j)] = j+1; // Record the index of the next character.
}
return maxLength;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| /*
The basic idea is that if you are robbing house i, the maximum loot may come from by robbing the i-2th house or by robbing the i-3th house. Therefore rob both and then find the path that gave the maximum profit.
Example: loot = [1,9,3,8,4,3,6,4,3,5,7,6]
Profit DP = [1,9,4,17,13,20,23,24,26,29,33,35]
Here,
dp[2] = loot[2] + loot[1]
dp[4] = loot[4] + max(dp[2], dp[1])
dp[5] = loot[5] + max(dp[3], dp[2]) and so on.
In the end, just compare the last two elements to check which path gave us the maximum profit.
Some people might not prefer modifying the original nums array. In that case, you can initialize another dp array of same length, initialize the first two elements as dp[0] = nums[0] and dp[1] = nums[1] and dp[3] = nums[0] + nums[2] and then performing the same loop. In that case, you would be using O(n) space.
*/
public int rob(int[] nums) {
if (nums.length == 0 || nums == null) // 3 Base Case
return 0;
if (nums.length == 1)
return nums[0];
else if (nums.length == 2)
return Math.max(nums[0], nums[1]);
else{
nums[2] = nums[0] + nums[2]; // House 3 profit is rob House 1 and 3.
for (int i = 3; i < nums.length; i++)
nums[i] = nums[i] + Math.max(nums[i-2], nums[i-3]);
return Math.max(nums[nums.length-1], nums[nums.length-2]);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| public boolean isHappy(int n) {
return isHappyConstantSpace(n); // Much faster than set method
//return isHappySet(n);
}
private boolean isHappyConstantSpace(int n){
int numSeenLessThan10 = 0; // If I see 10 single digits, then it means that I am
while (n != 1){ // now starting to see repititions.
if (n < 10) // Each time I see a num < 10, increment the counter
numSeenLessThan10++;
if (numSeenLessThan10 > 9)
return false;
n = getSquare(n); // Get the total of square of its digits.
}
return true;
}
/*
The general idea is that the moment you see a repition, it can't be a happy number, so keep track of digit square obtained so far. If they hit 1, well and good, otherwise there will be some repition, so return false.
*/
private boolean isHappySet(int n){
HashSet<Integer> seen = new HashSet<>(); // Keep track of numbers
while (true){
n = getSquare(n); // Get the sum of digits square
if (n == 1) // If it's 1, it's a happy number
return true;
else if (seen.contains(n)) // If it's a repition of something
return false; // seen before, it's not a happy no.
else
seen.add(n); // If not seen, add it.
}
}
private int getSquare(int n){ // Add the squares of the digits.
int total = 0;
while (n != 0){
int digit = n % 10;
total += digit * digit;
n /= 10;
}
return total;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
| public ListNode removeElements(ListNode head, int val) {
while (head != null && head.val == val) // While head contains the val, skip
head = head.next; // the head
ListNode current = head;
while (current != null && current.next != null){ // While we have something to iterate
if (current.next.val == val) // If current's val match, skip the
current.next = current.next.next; // next node.
else
current = current.next; // Else advance to the next node.
}
return head;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public int countPrimes(int n) {
if (n < 2)
return 0; // No prime numbers for numbers < 2
boolean[] store = new boolean[n]; // Using Sieve of Eratosthenes
for (int i = 2; i*i <= n; i++) // Start from i = 2 to sqrt(n)
if (!store[i]) // If store[i] = false, then mark all its
for (int j = i*i; j < n; j += i)// multiples in the store as true
store[j] = true; // True = not a prime, false = prime
int count = 0;
for (int i = 2; i < n; i++) // Loop through the array, count
if (!store[i])
count++;
return count;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public boolean isIsomorphic(String s, String t) {
if (s.length() != t.length()) // Can't be isomorphic is string lengths do not
return false; // match
char[] hashS = new char[128]; // To store String s' match
char[] hashT = new char[128]; // To store String t's match
for (int i = 0; i < s.length(); i++){
char charS = s.charAt(i), charT = t.charAt(i);
if (hashS[charS] != hashT[charT]) // If the values at respective characters index
return false; // do not match, return false
hashS[charS] = (char)(i+1); // Otherwise, mark those index with the same
hashT[charT] = (char)(i+1); // arbitrary value. I chose a simple (i+1) to
} // to mark both the hash with the same value.
return true; // Everything worked out, return true;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| // Recursive
public ListNode reverseList(ListNode head) { // Very tricky. Refer to the demo below
if (head == null || head.next == null)
return head;
ListNode node = reverseList(head.next);
head.next.next = head;
head.next = null;
return node;
}
//Iterative
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null)
return head; // No point in reversing empty or 1-sized list
ListNode curr = head, prev = null;
ListNode nextNode;
while (curr != null){ // While we haven't reached the tail
nextNode = curr.next; // Store the next node
curr.next = prev; // Current's next becomes it's previous
prev = curr; // Advance previous to current.
curr = nextNode; // Make current the actual next node
}
return prev; // Current is at null, so it's previous is the
} // new head.
|
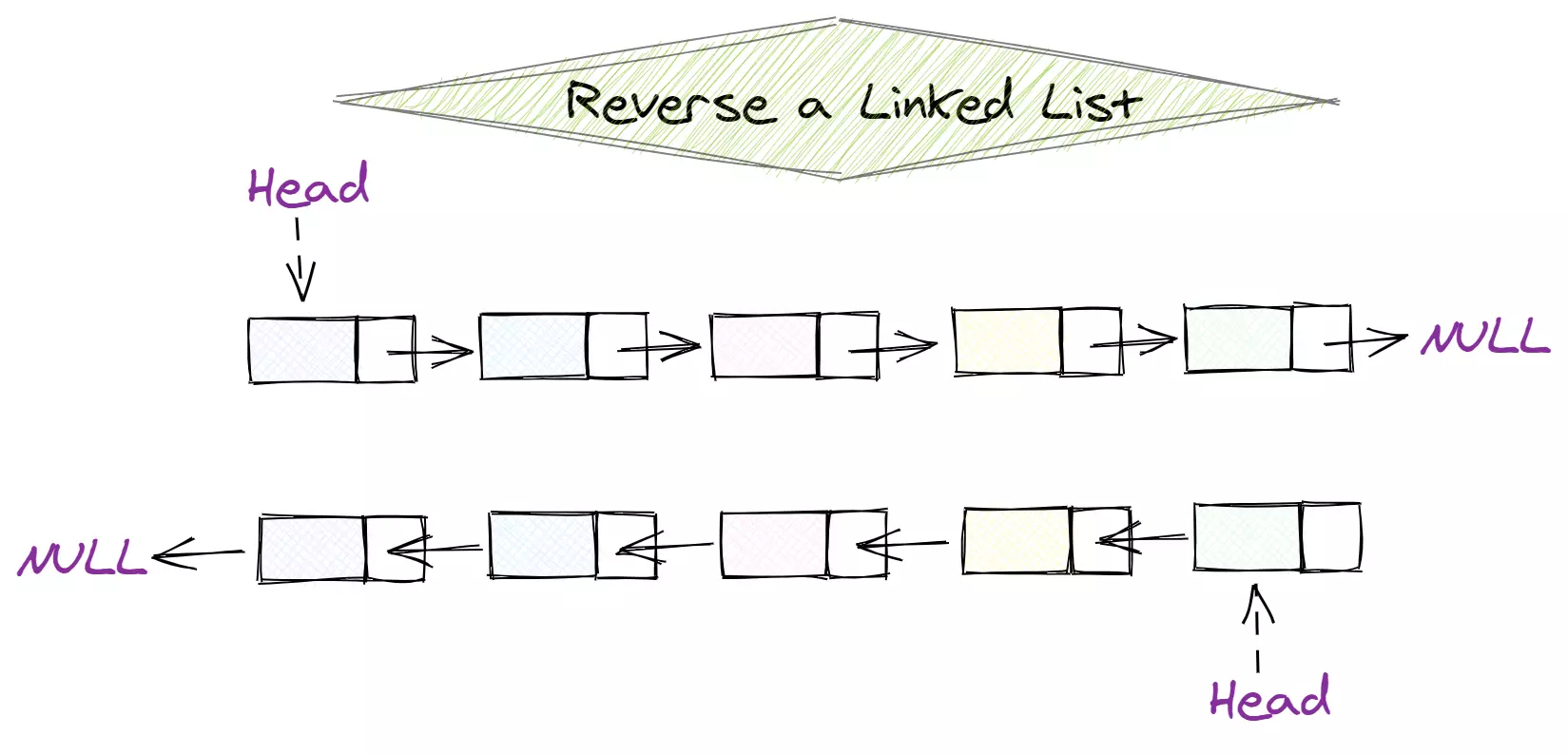
1
2
3
4
5
6
7
8
9
10
| public boolean containsDuplicate(int[] nums) {
if (nums.length < 2)
return false; // There can't be any duplicates.
HashSet<Integer> store = new HashSet<>(); // Store unique values.
for (int n: nums){
if (!store.add(n)) // Add func returns true if n was'nt present,
return true; // false if duplicate. Therefore if it was a
} // duplicate, return true.
return false; // No duplicates, so return false
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public boolean containsNearbyDuplicate(int[] nums, int k) {
if (nums.length < 2)
return false;
int left = 0, right = 0;
HashSet<Integer> store = new HashSet<>(); // Use a rotating window of size k
while (right < nums.length){ // While we haven't processed everything
if (store.contains(nums[right])) // If our current window contains duplicate
return true;
store.add(nums[right]); // No duplicates in the window
right++; // Increase right to visit the new element
if (right - left > k){ // If window becomes > k
store.remove(nums[left]); // remove the number on the left side of
left++; // the window and increase the left counter
} // for new window from the next index
}
return false; // No duplicates found in any window.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class MyStack {
Deque<Integer> stack;
/** Initialize your data structure here. */
public MyStack() {
stack = new ArrayDeque<>();
}
/** Push element x onto stack. */
public void push(int x) {
stack.add(x);
}
/** Removes the element on top of the stack and returns that element. */
public int pop() {
return stack.removeLast();
}
/** Get the top element. */
public int top() {
return stack.peekLast();
}
/** Returns whether the stack is empty. */
public boolean empty() {
return stack.isEmpty();
}
}
|
1
2
3
4
5
6
7
8
9
10
| public TreeNode invertTree(TreeNode root) {
if (root == null)
return null;
TreeNode temp = root.left; // Swap the left and right nodes
root.left = root.right;
root.right = temp;
invertTree(root.left); // Then swap the subsequent trees of those nodes.
invertTree(root.right);
return root; // Return the original root.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| // Iterative
public int fib(int N) {
if (N < 2) // fib(0) = 0; fib(1) = 1
return N;
int f0 = 0, f1 = 1, fn = 0;
for (int i = 2; i <= N; i++){
fn = f0 + f1; // fib(n) = fib(n-1) + fib(n-2)
f0 = f1; // f0 becomes f1
f1 = fn; // f1 becomes fn
}
return f1;
}
// Dynamic Programming
private int fibDP(int N){
if (N < 2)
return N;
int[] dp = new int[N+1]; // To store intermediate result
dp[1] = 1; // fib(0) = 0; fib(1) = 1
for (int i = 2; i <= N; i++)
dp[i] = dp[i-1]+dp[i-2]; // fib(i) = fib(i-1) + fib(i-2)
return dp[N]; // Return the last number in the array
}
|
- The minheap algorithm has $O(n lg n) $ complexity and $O(1)$ space. The idea here is that we use a minheap to keep only the k greatest elements. If size becomes more than k, we remove the smallest element at the top of the heap. Thereby, at the end, our kth largest element will be at the top.
- QuickSelect Algorithm performs in $O(n)$ best case, $O(n^2)$ worst case when the pivot chosen is always the largest, so we use a random pivot.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| // MinHeap Algorithm
public int kthLargest(int[] nums, int k){
PriorityQueue<Integer> q = new PriorityQueue<>((n1,n2) -> n1 - n2); // Initialize minheap
for (int n: nums){
q.add(n); // Add number one by one
if (q.size() > k) // If size is greater than k
q.poll(); // Remove the topmost element
}
return q.poll(); // The topmost element is our answer
}
// QuickSelect Algorithm - Hoare's Partition Scheme
private int[] arr;
public int kthLargest(int[] nums, int k){
arr = nums;
return quickselect(0, nums.length-1, nums.length-k);// kth largest is (n-k)th largest
}
private int quickselect(int left, int right, int k){
if (left == right) // Array contains only 1 element, that's the answer
return arr[left];
Random rand = new Random(); // Choose a random pivot between left and right
int pivotIndex = left + rand.nextInt(right-left); // but not left
pivotIndex = partition(left, right, pivotIndex); // Partition, and find it's correct index
if (k == pivotIndex) // That index is equal to kth statistic
return arr[pivotIndex];
else if (k < pivotIndex) // If it's less than the index, our ans lies in the
return quickselect(left, pivotIndex-1, k); // left side
else
return quickselect(pivotIndex+1, right, k); // Otherwise, it's on the right side.
}
private int partition(int left, int right, int pivotIndex){
int pivot = arr[pivotIndex]; // Partition element
swap(pivotIndex, right); // Move that element to the end
int wall = left - 1; // wall is initially before everything
for (int i = left; i < right; i++){
if (arr[i] < pivot) // If the current element is < than the pivot, then
swap(i, ++wall); // we need to swap it with the element next to wall.
}
swap(right, ++wall); // Lastly, swap the element at wall and the end.
return wall;
}
private void swap(int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
|
1
2
3
4
5
6
7
8
9
10
| public boolean isPowerOfTwo(int n) {
if (n < 1)
return false; // n < 0 cannot be powers of 2
while (n > 2){
if (n % 2 != 0) // If n is odd, it can't be a power of 2.
return false;
n = n / 2; // It is a multiple of 2, so divide it by 2.
}
return true; // n came out to be 1 which is a power of 2, so return true.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
| private char[][] board;
public boolean isValidSudoku(char[][] board){
this.board = board;
return rowCheck() && colCheck() && boxCheck(); // Check row first, then column and at
} // last, boxes because they are time
// consuming.
private boolean onePassCheck(){
HashSet<Integer>[] rows = new HashSet[9]; // 1 HashSet for each row
HashSet<Integer>[] columns = new HashSet[9]; // 1 HashSet for each column
HashSet<Integer>[] boxes = new HashSet[9]; // 1 HashSet for each box.
for (int i = 0; i < 9; i++){
rows[i] = new HashSet<>();
columns[i] = new HashSet<>();
boxes[i] = new HashSet<>();
}
for (int i = 0; i < 9; i++){
for (int j = 0; j < 9; j++){
int n = (int)(board[i][j]);
if (n != -2){ // -2 = '.'
int boxIndex = (i/3) * 3 + j/3; // Calculate which box we are in.
if (!rows[i].add(n) || !columns[j].add(n) || !boxes[boxIndex].add(n))
return false; // If the row set or the column set or the
} // box set contains that val, return false.
}
}
return true;
}
private boolean rowCheck(){ // Horizontal check
boolean[] arr;
for (char[] row: board){
arr = new boolean[9];
for (char c: row){
int val = c-'0';
if (val != -2){ // val = -2 means '.' in the board
if (arr[val-1]) // If val already seen, invalid sudoku
return false;
arr[val-1] = true; // else, Mark that index as seen.
}
}
}
return true;
}
private boolean colCheck(){ // Vertical Check.
boolean[] arr;
for (int col = 0; col < board.length; col++){
arr = new boolean[9];
for (int row = 0; row < board[0].length; row++){
int val = board[row][col]-'0';
if (val != -2){
if (arr[val-1])
return false;
arr[val-1] = true;
}
}
}
return true;
}
private boolean boxCheck(){ // For the 9 sub boxes, let the single
for (int i = 0; i < 9; i+=3){ // box checker check it's validity.
for (int j = 0; j < 9; j+=3) // If any of the subbox was invalid,
if (!singleBoxCheck(i,j)) // we abort and return false.
return false;
}
return true;
}
private boolean singleBoxCheck(int topRightRow, int topRightCol){
boolean[] arr = new boolean[9];
for (int i = 0; i < 3; i++){ // Each sub box has 3 rows and 3 columns
for (int j = 0; j < 3; j++){
int val = board[topRightRow+i][topRightCol+j]-'0'; // This gives us the value at
if (val != -2){ // each cell in the sub box and we fill the
if (arr[val-1]) // arr with all values that are seen.
return false; // If seen twice, return false;
arr[val-1] = true;
}
}
}
return true;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| /*
Since we reverse stack1 into stack2, stack2 is basically our queue, so if stack2 isn't empty, then the topmost element is what we need when we pop or peek. If it is empty, then again fill it with whatever's there is stack1, and it again becomes the correct queue.
*/
Stack<Integer> stack1;
Stack<Integer> stack2;
public MyQueue() {
stack1 = new Stack<>();
stack2 = new Stack<>();
}
public void push(int x) {
stack1.push(x); // Push onto stack1
}
public int pop() {
peek(); // First call the peek function, to make sure stack 2 isn't
return stack2.pop(); // empty. Then, the topmost element of stack2 is what we want
}
/** Get the front element. */
public int peek() {
if (stack2.isEmpty()){
while (!stack1.isEmpty())
stack2.push(stack1.pop());
}
return stack2.peek(); // stack2 is basically the queue, so return whatever's on the top
}
/** Returns whether the queue is empty. */
public boolean empty() {
return stack1.isEmpty() && stack2.isEmpty();
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| public boolean isPalindrome(ListNode head) {
if (head == null || head.next == null) // Size 0 or 1 list, must be unique.
return true;
if (head.next.next == null) // Size 2 list, compare the head and tail
return head.val == head.next.val; // values
ListNode middleNode = head; // Standard Rabbit-Tortoise pointers.
ListNode fastPointer = head; // Fast pointer jumps twice so by the time
// it reaches the end of the list, middlenode
ListNode curr = head; // is at the middle of the linkedlist.
ListNode prev = null;
ListNode nextNode; // These three nodes are for reversing the
// first half of the list
while (fastPointer != null && fastPointer.next != null){
middleNode = middleNode.next; // Advance middle once, fastpointer twice
fastPointer = fastPointer.next.next;
nextNode = curr.next; // Reverse the curr node, but first store the
curr.next = prev; // next newNode. By doing this, we would have
prev = curr; // reversed exactly half of the list because
curr = nextNode; // fastpointer advacnes at double the speed.
}
if (fastPointer != null) // If faspointer isn't null, then we have an
middleNode = middleNode.next; // odd length list, so advance middle once,
// List looks like 1->2->3->2->1 instead of
while (middleNode != null){ // 1->2->3->3->2->1
if (middleNode.val != prev.val) // While middle isn't null, check middlenode
return false; // val and prev val. Prev is basically the
middleNode = middleNode.next; // the point where the list reverses.
prev = prev.next; // Advance middle and next.
}
return true; // Values matched, so return true.
} // Reversed list looks like this:
// 1<-2<-3<-prev middle->3->2->1 in even len
// 1<-2<-prev middle->2->1 in odd lengths.
|
1
2
3
4
| public void deleteNode(ListNode node) {
node.val = node.next.val; // Node's value becomes its next node's value
node.next = node.next.next; // Node's next is it's next's next.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
| public boolean isAnagram(String s, String t) {
if (s.length() != t.length()) // Can't be anagram if size aren't the same
return false;
int[] store = new int[26]; // Acts like a hashmap
for (int i = 0; i < s.length(); i++) // Increment the count by 1 in the store for the
store[s.charAt(i)-'a']++; // index = position of char in the alphabet
for (int i = 0; i < t.length(); i++){ // Loop throught the second string, decrement
if (--store[t.charAt(i)-'a'] < 0) // count of each character in store by 1, but if
return false; // it goes below 0, then it means that character
} // occurred more than it did in s. So false.
return true; // Everything matched, so return true.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| List<String> paths = new ArrayList<>();
public List<String> binaryTreePaths(TreeNode root) {
if (root == null) // No paths
return paths;
String rootval = root.val + ""; // Converting int to string.
traverse(root, rootval);
return paths;
}
private void traverse(TreeNode root, String s){
if (root.left == null && root.right == null) // It's a leaf, and you found a path
paths.add(s); // so add it to the list
if (root.left != null) // Left side is traversable, so
traverse(root.left, s + "->" + root.left.val); // visit it and record its value.
if (root.right != null) // Same as above, but for right side.
traverse(root.right, s + "->" + root.right.val);
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| private int constantTime(int n){
if (n < 10)
return n; // Already a single digit
int result = n % 9;
if (result == 0) // If perfectly divisible by 9, then sum will be 9.
return 9;
return result; // Otherwise, the result is going to be n % 9.
}
private int iterative(int num){
while (num > 9){ // While number isn't between 2-9
num = sumOfDigits(num); // make num = sum of it's digits.
}
return num;
}
private int sumOfDigits(int n){ // Standard method to add the digits of a number.
int sum = 0;
while (n != 0){
sum += n % 10; // Extract the last digit, add it to sum.
n /= 10; // Divide the num by 10.
}
return sum;
}
|
1
2
3
4
5
6
7
8
| public int largestPerimeter(int[] A) {
Arrays.sort(A); // Sort so the largest sides are at the end.
for (int i = A.length-3; i >= 0; --i) // Triangle inequality Theorem : a + b > c
if (A[i] + A[i+1] > A[i+2]) // If sum of last two is greater than the last
return A[i] + A[i+1] + A[i+2]; // we found out max perimeter, otherwise
return 0; // decrease i by i, then check the next three
} // triplets
// In the end if nothing works out, we return 0.
|
1
2
3
4
5
6
7
8
9
10
11
| public boolean isUgly(int num) {
if (num < 1)
return false; // Negative numbers are automatically non ugly
while (num % 2 == 0) // Keep dividing number by 2 till it is divisible
num /= 2;
while (num % 3 == 0) // Keep dividing by 3
num /= 3;
while (num % 5 == 0) // and 5
num /= 5;
return num == 1; // If num isn't 1, that means that there are other prime factors
} // except 2,3 and 5.
|
1
2
3
4
5
6
7
| public int missingNumber(int[] nums) { // Since it's given that the array contains
int nsum = (nums.length*(nums.length+1))/2; // all numbers from 0-n, we use the formula
int arraySum = nums[0]; // to compute sum of n numbers.
for (int i = 1; i < nums.length; i++) // Then we loop through the array to compute
arraySum += nums[i]; // the sum of the array.
return nsum - arraySum; // Subtract the array sum from the required
} // sum, and that gives us the missing number
|
1
2
3
4
5
6
7
8
9
10
11
12
| public int firstBadVersion(int n) { // Basic Binary Search Algorithm
int low = 1, high = n;
int mid;
while (low < high){
mid = low + (high - low)/2; // high - low to prefent integer overflow.
if (isBadVersion(mid)) // if the model at mid was bad version, then we
high = mid; // could possibly have a bad version before it
else
low = mid+1; // If it wasn't, then our first bad version lies
} // beyond the middle element.
return low;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| /*
The general idea is that we know the end of the array is going to contain zeroes. So first, iterate over the array, if you find any non-zero value, copy it down to the front of the array. Then we you are done, length of the array minus the last index where you copied the non-zero element is the number of zeroes you need to fill in. So iterate from that last non-zero index to the end of the array and fill in zeroes.
*/
public void moveZeroes(int[] nums) {
int lastNonZeroIndex = 0;
for (int i = 0; i < nums.length; i++)
if (nums[i] != 0)
nums[lastNonZeroIndex++] = nums[i];
for (int i = lastNonZeroIndex; i < nums.length; i++)
nums[i] = 0;
}
/*
This solution is an extension of the above, but a better one because we only swap elements when needed and do not do any unnecessary writes. Start from the beginning of the array, maintain the last position of non-zero value you saw, and the current element. If you see a non-zero value, swap the current value with the index just after the last non-zero index you have, and then increment the non-zero index by 1 because you just found a new non-zero value. This helps us prepare for the next non-zero value we find and copy it at this index+1. By doing so, we are basically partitioning the array into non-zeroes and zero values.
*/
public void moveZeroes(int[] nums) {
for (int lastNonZeroIndex = 0, i = 0; i < nums.length; i++){
if (nums[i] != 0)
swap(nums, i , lastNonZeroIndex++);
}
}
private void swap(int[] a, int i, int j){
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public boolean wordPattern(String pattern, String str) {
String[] words = str.split(" "); // Split str into words
if (pattern.length() != words.length) // If length of pattern and words mismatch
return false; // then pattern do not match
HashMap<Character, String> patternStore = new HashMap<>(); // Map pattern char to word
HashMap<String, Character> wordMap = new HashMap<>(); // Map word to pattern char
for (int i = 0; i < words.length; i++){
char c = pattern.charAt(i); // Get the char
patternStore.putIfAbsent(c, words[i]); // Put it in patternStore if absent
if (!patternStore.get(c).equals(words[i])) // If it was already there and it doesn't
return false; // map to words[i], we have a violation
wordMap.putIfAbsent(words[i], c); // Now check the other way around. If
if (wordMap.get(words[i]) != c) // words is absent in the map, map it to
return false; // the char. If present, then fetch it's
} // mapping and check if both match to c.
return true; // No violation, so return true
}
|
1
2
3
| public boolean canWinNim(int n) {
return n % 4 != 0; // You can always win the game if n is not divisible by 4.
}
|
1
2
3
4
5
6
7
| public boolean isPowerOfThree(int n) {
if (n < 1) // If negative, it can't be a power of 3.
return false;
while (n % 3 == 0) // While n is divisible by 3, keep dividing it.
n /= 3;
return n == 1; // In the end, if it was a power of 3, then n should be 1.
}
|
1
2
3
4
5
6
7
| /*
You can also use the iterative method that I have used in Power of Two and Power of Three problems. I just wanted to try a different approach here. This is a constant time function.
*/
public boolean isPowerOfFour(int num) {
double pow = Math.log(num)/Math.log(4); // Calculate x in 4^x = num using logs.
return pow == (int)pow; // Making sure that x is an integer and not a
} // fractional exponent.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| /*
1 Liner solution. Basically, create a StringBuilder of the string, the builder already has a reverse method, so reverse it and then return it's toString.
*/
public String reverseString(String s) {
return new StringBuilder(s).reverse().toString();
}
/*
Golfing aside, here is how one is expected to solve it in an interview.
*/
public String reverseString(String s) {
char[] array = s.toCharArray(); // Create a char array of the string
int len = array.length; // length of the array
for (int i = 0; i < len/2; i++){ // We only need to iterate over half the array.
char temp = array[i]; // Swap the 0th index element with (len-1)th,
array[i] = array[len-i-1]; // 1st index element with (len-2)th, until you get
array[len-i-1] = temp; // to the middle element.
}
return new String(array); // Return a new string with the reversed array.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| /*
The basic idea here is that you only need to iterate haystack length - needle length, and then check the substring of size = needle length in haystack from each index. If you are successfully able to match each character of the needle in the corresponding substring in haystack, return the index you start from.
*/
public int strStr(String haystack, String needle) {
if (needle.length() > haystack.length()) // Needle length can't be > than haystack
return -1;
int hl = haystack.length();
int nl = needle.length();
if (nl == 0) // Empty strings are always a match starting
return 0; // from 0.
for (int i = 0; i <= hl-nl; i++){ // Iterate haystack length - needle length.
for (int j = 0; j < nl && haystack.charAt(i+j) == needle.charAt(j); ++j)}
if (j == nl-1) // We are checking how far from i can we
return i; // match. If i matched with j, increment j
} // and then match the character i+1 to j.
} // If that matches, increment j and match i+2
return -1; // j == n-1 checked wether or not if we were
} // able to match the full needle string, if
// yes, then i is our index
// in the end, nothing matched, so return -1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| public String reverseVowels(String s) {
if (s.length() < 2)
return s; // No need to reverse a string of length 0 or 1
char[] str = s.toCharArray(); // Get the char array
int left = 0;
int right = str.length-1;
while (left < right){
while (left < right && !isVowel(str[left])) // While left is pointing to a
left++; // consonant, increment it/
while (left < right && !isVowel(str[right])) // While right is pointing to a
right--; // consonant, decrement it.
char temp = str[left]; // Left and right are now pointing
str[left] = str[right]; // to vowels, so swap it.
str[right] = temp; // And then increment left and
left++; // decrement right to process the
right--; // inner string
}
return new String(str); // Return a string from the reveresed array.
}
private boolean isVowel(char c){ // Function to check if a character is a vowel.
switch (c) {
case 'a':
case 'e':
case 'i':
case 'o':
case 'u':
case 'A':
case 'E':
case 'I':
case 'O':
case 'U':
return true;
default:
return false;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public int[] intersection(int[] nums1, int[] nums2) {
Set<Integer> set1 = new HashSet<Integer>(); // Record all unique values in set 1
for (int i: nums1)
set1.add(i);
Set<Integer> intersect = new HashSet<>(); // We will use it to record intersection
for (int i: nums2) // For each value in nums2 array
if (set1.contains(i)) // If set1 contains it, we found an
intersect.add(i); // intersecting element, so add it.
int[] res = new int[intersect.size()]; // We will now convert the set to an
int i = 0; // array and then return the array.
for (int n: intersect)
res[i++] = n;
return res;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| /**
The basic idea here is to close in on the square root using binary search algorithm.
I handle 4 seperately because it's root is the only one where 4/3 < it's square root.
All other numbers square root is greater than its value/3.
So we create a lowerBound of 1 and an upperBound of num/3. Then if the middle value's square
overshoots, we make upperBound = mid-1, otherwise increment lowerBound to mid+1. This way, we
close on the square root from both sides, and if the middle values is the square root, it's
square will yield num.
*/
public boolean isPerfectSquare(int num) {
if (num < 2 || num == 4)
return true;
long lowerBound = 1;
long upperBound = num/3;
long mid;
long square;
while (lowerBound <= upperBound){
mid = lowerBound + (upperBound-lowerBound)/2;
square = mid*mid;
if (square == num)
return true;
if (square > num)
upperBound = mid-1;
else
lowerBound = mid+1;
}
return false;
}
|
I cannot explain it better than this post.
1
2
3
4
5
6
7
8
9
10
11
| public int getSum(int a, int b) {
if (a == 0)
return b;
if (b == 0)
return a;
int sum = a ^ b;
int carry = a & b;
if (carry == 0)
return sum;
return getSum(sum, carry << 1);
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| public int guessNumber(int n) { // Standard binary search algorithm
int low = 1, high = n, result = -2; // Arbitrary result, but not 0
int mid = 0;
while (result != 0){
mid = low + (high-low)/2; // Check the mid.
result = guess(mid); // Check if our guess is correct
if (result == -1) // If result == -1, then we overshot
high = mid-1; // So we can discard all values > mid
else if (result == 1) // If result == 1, we undershot
low = mid+1; // Need to discard all the values < mid
}
return mid; // Result == 0, so return the mid.
}
|
1
2
3
4
5
6
7
8
9
10
| public boolean canConstruct(String ransomNote, String magazine) {
int[] store = new int[26];
for (char c: magazine.toCharArray()) // First, fill the store with available
store[c-'a']++; // characters from the magazine
for (char c: ransomNote.toCharArray()) // Then, scan through the note, decrement
if (--store[c-'a'] < 0) // each char's index by 1 because we used
return false; // it. If it's frequency drops below 0,
return true; // then it means that we need more chars
} // than available. In the end, return
// true if everything worked out.
|
1
2
3
4
5
6
7
8
9
10
| public int firstUniqChar(String s) {
int[] freq = new int[26]; // Preprocess freq array to maintain freq of each
char[] chars = s.toCharArray(); // character in the string s
for (char c: chars)
++freq[c-'a'];
for (int i = 0; i < chars.length; i++) // Make a second pass through the chars of the
if (freq[chars[i]-'a'] == 1) // string in order, and if any of the char's
return i; // frequency is 1, that's our unique char
return -1; // Otherwise, no unique character
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| /**
The general idea here is same as the problem where we are required to find a unique int
in an array containing duplicates except one. We use the xor operator between each character
of the string s and t, and the ones that are duplicate will xor to give 0. XOR of any element
with 0 is the element itself, and XOR of two same elements gives 0. This way, since string s
and t basically has pairs of repeating characters except one, the unique element will XOR
with 0 and give us it's ASCII code. The only thing we need to take care of is to now shift it
up by 26, so we add 'a' and convert it to char.
*/
public char findTheDifference(String s, String t) {
int xor = 0;
for (char c: s.toCharArray())
xor ^= c-'a';
for (char c: t.toCharArray())
xor ^= c-'a';
return (char)(xor+'a');
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| /**
Notice that # of digits between 0-9 is 1*9, 10-99 is 2*90, 100-999 is 3*900. If we generalize
it, it is exactly equal to 9 * (num of digits in the number) * 10^{# of digits - 1}.
*/
public int findNthDigit(int n) {
if (n < 10)
return n;
int pow = 1; // First we need to figure out how many digits there are
long upperBound = 9; // in the number.
while (n > upperBound){
n -= upperBound; // If n is a two digit number, subtract the 9 single digit
++pow; // numbers, if 3 digit, subtract the first 189 digits.
upperBound = (long)Math.pow(10, pow-1) * pow * 9;
} // pow allows us to track how many digits there are in num.
int num = (int)Math.pow(10,pow-1) + (n-1)/pow; // Calculate which number we want
int position = pow - 1 - (n-1) % pow; // Calculate which index we want
for (int i = 0; i < position; i++) // Divide num that many times
num /= 10;
return num % 10; // num % 10 gives us that digit.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public int sumOfLeftLeaves(TreeNode root) {
if (root == null) // Empty tree, therefore total is 0.
return 0;
int sum = 0; // Initialize sum.
// Look ahead and check. If left is not null but left is a leaf, then sum is the value of the left leaf.
// But if left is null or left is an inner node, then we need to explore it, so sum is whatever the subtree from the left node returns.
if (root.left != null && root.left.left == null && root.left.right == null)
sum = root.left.val;
else
sum = sumOfLeftLeaves(root.left);
// We computed the sum of the left side. Now we need to traverse the right side and fetch
// the sum, so total sum is sum of the left side as computed above + sum returned by
// traversing the right side.
return sum + sumOfLeftLeaves(root.right);
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public int longestPalindrome(String s) {
int[] freq = new int[128]; // To record the frequency of each char
for (char c: s.toCharArray())
freq[c]++; // Increment count by 1 for each character observed
int len = 0; // length of the longest palindrome
boolean isOdd = false; // Check if our palindrome length is odd
for (int i = 0; i < 128; i++){ // Go through each character's index
if (freq[i] != 0){ // Only if it has been observed atleast once
int val = freq[i]; // Store it's frequency
int used; // Record how many of it's occurrences we will use
if (val % 2 == 0) // If a perfect multiple of 2, we will use all
used = val;
else{
used = val-1; // If odd occurrences, then the max we can use to form a
isOdd = true; // valid palindrome is val-1. It also tells us that the
} // palindrome is going to be of odd length.
len += used; // Finally, increment length by the number of chars used
}
}
if (isOdd) // If length is odd, we can always insert any single
return len+1; // character in the middle to keep the palindrome valid.
return len; // If the length is even, then we can't do anything.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public List<String> fizzBuzz(int n) {
List<String> nums = new ArrayList<String>();
for (int i = 1; i <= n; ++i){ // Loop from 1 to n
if (i % 15 == 0) // If i divisible by 15, add "FizzBuzz"
nums.add("FizzBuzz");
else if (i % 5 == 0) // i's not a multiple of 15, check if it's a
nums.add("Buzz"); // multiple of 5. If so, add "Buzz"
else if (i % 3 == 0) // i's not a multiple of 5, check if it's a
nums.add("Fizz"); // multiple of 3, if so, add "Fizz"
else
nums.add(i+""); // Otherwise, just add the String type of the
} // number
return nums;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| public int thirdMax(int[] nums) {
if (nums.length == 0) // Empty array
return 0;
if (nums.length == 1) // Size 1 array
return nums[0];
if (nums.length == 2) // Size 2 array, check between 0th element or 1st element
return nums[0] > nums[1] ? nums[0] : nums[1];
long firstMax = Long.MIN_VALUE; // Lowest values for all three
long secondMax = Long.MIN_VALUE;
long thirdMax = Long.MIN_VALUE;
for (int i: nums){ // For each number in the array
if (i > firstMax){ // If num > than the largest, then old largest
thirdMax = secondMax; // becomes second largest and second largest becomes
secondMax = firstMax; // first largest, then update the largest.
firstMax = i;
}
else if (i > secondMax && i != firstMax){ // If num > second and num is not is the
thirdMax = secondMax; // same as first, first largets becomes
secondMax = i; // second largest and update the second
}
else if (i > thirdMax && i != secondMax && i != firstMax) // // If num > third, we
thirdMax = i; // need to check that it is not the same
} // as the first and second largest.
if (thirdMax == Long.MIN_VALUE) // This check allows us to make sure that
return (int)firstMax; // we do indeed have a third max and is
return (int)thirdMax; // not what we initialized initially.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| public String addStrings(String num1, String num2) {
if (num1.equals("0"))
return num2;
if (num2.equals("0"))
return num1;
/** We use a char array to maintain the digit at each index. We want the array to be of
the size of the largest string + 1 to handle carry bit if any at the end. We start
adding each digit of the string from the end, and place it in it's correct index at the
end of the sum array. This way, we avoid reversing it and return the answer in constant
time. Take care to convert the digit you compute by adding '0'. Lastly, if the carry bit
is 1, we need to make the 0th index as 1, and return the string by using the sum array.
If it's not 1, then the sum array has a leading 0 which we don't want. So we use Java's
String constructor that takes in the char array, startingIndex in that array and the
number of elements of that array we want. So if the carry isn't 1, we technically want
everything from index 1 and # of elements = sum.length - 1 because we discard 0 index.
*/
char[] sum = new char[1 + Math.max(num1.length(), num2.length())];
int index = sum.length-1, idx1 = num1.length()-1, idx2 = num2.length()-1, carry = 0, total = 0;
int n1, n2;
while (idx1 >= 0 || idx2 >= 0){
n1 = idx1 < 0 ? 0 : num1.charAt(idx1--)-'0';
n2 = idx2 < 0 ? 0 : num2.charAt(idx2--)-'0';
total = n1 + n2 + carry;
carry = total/10;
sum[index--] = (char)(total % 10 + '0');
}
if (carry == 1){
sum[0] = '1';
return new String(sum);
}
return new String(sum, 1, sum.length-1);
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| private int[][] grid; // Store it once, instead of passing it over & over.
public Node construct(int[][] _grid) {
grid = _grid;
return helper(0,0,grid.length); // Ask helper to build the tree.
}
private Node helper(int top, int left, int len){
if (len <= 0) // Base case: if empty grid or if we are done
return null; // checking the full grid, return null
int key = grid[top][left]; // Get the topleft value, and start checking the box
for (int i = 0; i < len; ++i){ // of len*len. If at any point, the value doesn't
for (int j = 0; j < len; ++j){ // match the key, we have found a breakpoint from
if (grid[top+i][left+j] != key){ // where we need to break the grid into four
int offset = len/2; // grids, each of len = len/2. The topleft grid has
return new Node(true, false, // the same top and left point, the topright
helper(top,left, offset), // grid has left point shifted to
helper(top, left + offset, offset), // the right by offset.
helper(top+offset, left, offset), // The bottom left grid
helper(top+offset, left+offset, offset)); // is shifted
} // downwards by offset with the same left point. The bottom right grid will
} // have an index where it's top is shifted down by len/2 and left by left/2.
} // We know that the node will have a value = true if 1 else false and it won't be a leaf, so true, false, topleft, topright, bottomleft, bottomright.
return new Node(key == 1, true, null, null, null, null); // Everything passed, so we return a new Node whose value is true if key is 1, else false and it will be a leaf, with
// no children, so 4 nulls.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> res = new ArrayList<>(); // Result list
if (root == null) // If root is null, return empty list.
return res;
Queue<Node> q = new LinkedList<>(); // BFS Queue. Add the root.
q.add(root);
while (!q.isEmpty()){ // While q isn't empty
int size = q.size(); // Check how many elements in that level
List<Integer> level = new ArrayList<>(size);// level list to store elements.
for (int i = 0; i < size; i++){ // Remove each node for whatever the size
Node n = q.poll(); // Add that node's value and add all of
level.add(n.val); // its children to the queue.
for (Node child: n.children)
q.add(child);
}
res.add(level); // Add the level array to the result
}
return res; // Return the result list.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public int countSegments(String s) {
if (s.length() == 0) // Empty String
return 0;
int segments = 0; // Record segments
char prev = s.charAt(0); // We will compare adjacent characters.
for (int i = 1; i < s.length(); ++i){ // Start looking at chars from index 0
char curr = s.charAt(i); // Get the current char
if (prev != ' ' && curr == ' ') // If previous char wasn't a space but the
++segments; // current char is, we found a segment.
prev = curr; // Make previous = current for next iteration
}
/**
This line is important. If prev was an empty space, that means that all we have been looking
at was empty spaces towards the end. So return whatever segments we found in the beginning
of the string. But if prev wasn't a space, that means the char next to prev might have been
an empty space or just a normal character. In any case, we would want to include that last
segment, so we return segment+1.
*/
return prev == ' ' ? segments : segments+1;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> result = new ArrayList<>();
if (root == null) // Empty Tree
return result;
Queue<TreeNode> q = new LinkedList<>(); // BFS Queue
q.add(root);
while (!q.isEmpty()){ // While we have something to process
List<Integer> level = new ArrayList<>();
int size = q.size(); // Check how many elements at the current level
for (int i = 0; i < size; i++){
TreeNode node = q.poll(); // Remove one element each time
if (node != null){ // If not null, add it's val to the level list,
level.add(node.val); // and it's left and right children to the queue
q.add(node.left); // to process in order
q.add(node.right);
}
}
if (!level.isEmpty()) // If level list wasn't empty,
result.add(level); // add it to the result list.
}
return result;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| HashMap<Integer, Integer> sumToWays; // Record how many ways there are to form sum
int ways; // Total number of ways.
public int pathSum(TreeNode root, int sum) {
sumToWays = new HashMap<>();
ways = 0;
sumToWays.put(0,1); // 1 way to form a sum of 0.
helper(root, 0, sum);
return ways;
}
/**
The idea here is as follows. Start with the root node, and keep a running total. We maintain
how many ways there to form a running sum. Then we check how many ways there are to form
(running sum) - (sum we are looking for). If there is a way to form it, then we increase the
number of ways to form sum. We then have to update the map to record how many ways can the
running sum be formed. If it's something we could form before, increment it, or else set it
to 1. Now, traverse the left side and then the right side. In the end, for each time we
incremented the count for a running sum, we need to decrement it because we are backtracking.
We are first going down, incrementing the count for runningSum, then we move up and decrement
it by 1 for each time we observed it. This is to maintain the Pre-Order traversal.
*/
private void helper(TreeNode node, int runningSum, int sum){
if (node == null)
return;
runningSum += node.val;
ways += sumToWays.getOrDefault(runningSum-sum, 0);
sumToWays.put(runningSum, sumToWays.getOrDefault(runningSum, 0)+1);
helper(node.left, runningSum, sum);
helper(node.right, runningSum, sum);
sumToWays.put(runningSum, sumToWays.get(runningSum)-1);
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public List<Integer> findAnagrams(String s, String p) {
List<Integer> result = new ArrayList<>();
int start = 0, end = 0, slen = s.length(), plen = p.length();
if (slen == 0 || slen < plen || plen == 0)
return result;
int[] freq = new int[26]; // Store the freq of chars in p
for (char c: p.toCharArray())
freq[c-'a']++;
char[] sArr = s.toCharArray(); // Get the chars of the string s as an array
while (end < slen){ // While everything is not processed
if (--freq[sArr[end]-'a'] >= 0) // decrease the freq of the char at index end
plen--; // if it's > 0, then we matched something in p
// so decrease plen by 1.
while (plen == 0){ // If plen goes to 0, we were able to match all
if (end-start+1 == p.length()) // chars of p. If length of the matched chars is
result.add(start); // equal to length p, we found a start point.
if (freq[sArr[start]-'a'] >= 0) // Check if the freq of char at start index is
plen++; // >= 0. If it is, shift the window to the right
++freq[sArr[start++]-'a']; // but first restore the frequency of the char
} // at the index start.
end++; // Get ready to inspect the new element
}
return result; // Return the answer.
}
|
The idea is as follows. Sum of first n numbers is given by $\frac{n^2+n}{2}$. We need to find $n$ such that sum of $n$ numbers is closest to the number of coins we have. That is, $\frac{n^2+n}{2} = k$ where $k$ is the number of coins we have. So, everything boils down to solving the quadratic equation $n^2 + n - 2k = 0$. We use the quadratic formula where for any quadratic equation $ax^2 -bx + c$ is solved substituting for $a$, $b$ and $c$ in $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2}$. Here, $a$ and $b$ are always going to be 1, while $c$ is always going to be $2k$. Substitute those, and solve the equation.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public int arrangeCoins(int n) {
// return solveQuadratic(n);
return iterative(n);
}
private int solveQuadratic(int n){
return (int)(Math.sqrt(1 + 8*(long)n)-1)/2;
}
private int iterative(int n){
int used = 1, level = 0; // Coins used, and level completed.
while (n > 0){ // While coins left are greater than 0.
n-=used; // Calculcate remaining coins.
if (n > -1) // If there are still some coins left,
++level; // we were able to fill the level.
++used; // Prepare used for the next level, which is plus 1.
}
return level; // Return level
}
|
1
2
3
4
5
6
7
8
9
10
| public int hammingDistance(int x, int y) {
int diff = 0; // Track differences
while (x != 0 || y != 0) { // While both of them aren't 0
if (x % 2 != y % 2) // Check the bit of x and y by mod 2. If they are unequal
diff++; // increment difference.
x /= 2; // Divide x and y by 2.
y /= 2;
}
return diff;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| public int compress(char[] chars) {
int len = chars.length; // No need to reverse array of length 0 or 1
if (len < 2)
return len;
int arrayIndex = 0; // To maintain the length of new array.
int start = 0; // start index
int end = 0; // end index
while (end < len){
char first = chars[start]; // Record the char we are looking at.
int count = 0; // count is 0.
while (end < len && chars[end] == first){ // while the char is the same
++end; // increment end to check next char
++count; // and increment the count.
}
start = end; // shift start to end to check next sequence of chars
chars[arrayIndex++] = first; // our arrayIndex points to to the new array's
if (count != 1){ // indices. So copy the first char to arrayIndex.
if (count > 1 && count < 10) //Only if count isn't 1, if count is less than 10
chars[arrayIndex++] = (char)(count+'0'); // then we simply convert count to char and write it next to the char we just overwrote.
else // Otherwise, it has many digits. So convert it to
for (char c: String.valueOf(count).toCharArray()){ // string and add all it's digit to the array one by one while increment arrayIndex.
chars[arrayIndex++] = c;
}
}
}
return arrayIndex; // Wherever arrayIndex is, is the new length for the array.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public int numberOfBoomerangs(int[][] points) {
int boomerangs = 0;
HashMap<Double, Integer> map = new HashMap<>(); // To record points with same dist
for (int[] i: points){ // Compute distance between one point and every other.
map.clear() // clear map before each relative distance computation
for (int[] j: points){ // Compute distance with other points
if (i == j) // Don't compare the same two points.
continue;
double dist = Math.sqrt(Math.pow(i[0]-j[0],2) + Math.pow(i[1]-j[1],2));
int prevCount = map.getOrDefault(dist, 0); // Check how many points are equidistant from point i.
boomerangs += prevCount * 2; // Number of boomerangs = whatever pairs there were before times 2, because you can form twice the number of different orders.
map.put(dist, prevCount+1); // Increase the count of points observed for that distance.
}
}
return boomerangs; // return number of boomerangs
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| /**
The idea is simple. For each number in the array, since it's gauranteed that that the values
lie are inclusive [1,n], we can look at the index value-1. So check that index, and mark
that value as negative. That is why I take the absolute value. Check value at that index, if
negative, it means we have visited it via some other duplicate value. But if it's positive,
then we are seeing it for the first time, so make it's value negative. Make a second pass.
For values that are still positive, that means those indices were never visited, hence left
positive. So add 1 to them and add it to the set. Eg:
Given array a = [4,3,2,7,8,2,3,1],
1. val = 4 => idx = 3 & a[3] > 0, therefore, a[3] *= -1
a = [4,3,2,-7,8,2,3,1]
2. val = 3 => idx = 2 & a[2] > 0, therefore a[2] *= -1
a = [4,3,-2,-7,8,2,3,1]
3. val = -2 => idx = abs(-2)-1 = 1 & a[1] > 0, therefore a[1] *= -1
a = [4,-3,-2,-7,8,2,3,1]
4. val = -7 => idx = abs(-7)-1 = 6 & a[6] > 0, therfore a[6] *= -1
a = [4,-3,-2,-7,8,2,-3,1]
5. val = 8 => idx = abs(8)-1 = 7 & a[7] > 0, therfore a[7] *= -1
a = [4,-3,-2,-7,8,2,-3,-1]
6. val = 2 => idx = 1 but a[2] < 0. No change.
7. val = -3 => idx = abs(-3)-1 = 2 but a[2] < 0. No change.
8. val = -1 => idx = abs(-1)-1 = 0 & a[0] > 0, therefore a[0] *= -1
a = [-4,-3,-2,-7,8,2,-3,-1]
Observation: Notice index 4 and 5 have positive values, since those values were never
encountered, so the values at those indexes never became negative. Hence missing values are
5 and 6.
*/
public List<Integer> findDisappearedNumbers(int[] nums) {
List<Integer> result = new ArrayList<>();
for (int i: nums){ // For each number in the array
int idx = Math.abs(i)-1; // Look at the index that the number corresponds to
if (nums[idx] > 0) // If val is -ve, then it means we have encountered it.
nums[idx] *= -1; // If not, make it -ve.
}
for (int i = 0; i < nums.length; ++i)
if (nums[i] > 0) // Make another pass through the array, and the indices
result.add(i+1); // where value was positive, index+1 was missing from
return result; // the array
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| /**
We will employ a greedy algorithm where we first try to content children whose requirements
are small. We do this by sorting both the arrays, so we can match the child with least
requirement with the smallest cookie available.
*/
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int satisfied = 0, i = 0, j = 0;
while (i < g.length && j < s.length){ // While children are left and we have cookies,
if (s[j] >= g[i]){ // Check if the cookie at index j >= child i's requirement
satisfied++; // If so, increment the number of content child and we will
i++; // process the next child.
} // If cookie j < child i's demand, check the next cookie by
j++; // incrementing j. If cookie j > child i's demand, we will
} // still need to increment j, hence outside the conditional.
return satisfied; // Return number of satisfied children
}
|
Link to the solution explanation. This problem is phrased poorly and I had to read the comments by other users to understand what it required from me. The link I marked here explains the logic pretty good. But the simple logic is this: The number of rounds $r = \frac{Total Test Time}{Minutes To Die} +1$. Each pig has chances of dying in each round or staying alive till the end, so we plus 1. Now given the number of rounds $r$ and the number of samples $s$, how many volunteers $v$ will you need? $r^v = s$. Each round has some volunteers which in total at the end should be able to test out all the samples. Therefore, $v =\log_rs$.
1
2
3
4
| public int poorPigs(int buckets, int minutesToDie, int minutesToTest) {
int base = minutesToTest/minutesToDie+1; // How many rounds can you perform?
return (int)Math.ceil(Math.log(buckets)/Math.log(base));
}
|
1
2
3
4
5
6
7
8
9
10
11
| public int pivotIndex(int[] nums) {
int sum = 0, leftSum = 0; // We will test each index as a pivot by sliding it ->
for (int i: nums) // Precalculate the sum of the array
sum += i;
for (int i = 0; i < nums.length; ++i){ // Check if the sum of the leftSide of i is
if (leftSum == sum - leftSum - nums[i]) // equal to totalSum - leftSideSum - pivot
return i; // which is i. If so, return i.
leftSum += nums[i]; // Otherwise add nums[i] to the leftSum and
} // slide pivot to the ->.
return -1; // No pivot found. Return -1.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| public int[] sortedSquares(int[] A) {
int len = A.length; // Length of array A
int pivot = 0; // Pivot is the index where values goes from -ve to +ve.
while (pivot < len && A[pivot] < 0) // While values are -ve.
++pivot; // increment pivot. We exit when we find a positive.
int[] squares = new int[len]; // Result array
int index = 0; // Keeps track of where to where to put elements in result array
if (pivot == 0) // pivot = 0 means pivot didn't shift, there are only +ve values
for (int i: A) // So fill in the array with squares of numbers.
squares[index++] = i*i;
else{ // Otherwise we have a negative somewhere.
int left = pivot-1; // So we will compare values left and right of the pivot
int right = pivot; // and whichever's smaller fills up the array first.
while (left > -1 && right < len){
int lsquare = A[left] * A[left];
int rsquare = A[right] * A[right];
if (lsquare < rsquare){ // left < right, so add left square. decrement left
squares[index++] = lsquare;
--left;
}
else if (rsquare < lsquare){ // right < left, add right square and increment.
squares[index++] = rsquare;
++right;
}
else{
squares[index++] = lsquare; // both are equal. add both square and
squares[index++] = rsquare; // decrement left, increment right.
--left; // Continue doing this until we hit either end
++right; // of the array.
} // In the end we need to check if elements on
} // either side are left to be filled in.
while (left > -1) // Left side elements remain, so fill their
squares[index++] = A[left] * A[left--]; // squares one by one till none left.
while (right < len) // Right side elements remain, so fill their
squares[index++] = A[right] * A[right++]; // squares in
}
return squares;
}
|
We use the KMP Algorithm that allows us to match a string ’s’ with another string ‘p’ to find the longest sequence of characters in ’s’ that match ‘p’. We can use a Naive Pattern match where we start from the beginning of the string and start comparing the characters of ’s’ with ‘p’. Initially, we keep the partition at index 0. If the character’s match, we move partition to the right by 1 till we get to the end of the string. If something doesn’t match, we don’t move the partition but look at the next character to match. In the end, wherever the partition is, that’s our longest length we could match with string ‘p’. The complexity of that is O(len(p)(len(s)-len(p)+1)).
KMP fixes it by skipping characters that we know already match. In this problem, we aren’t matching with any other string but itself. So, we start from index 1 of the string and compare it from the beginning. If they match, we increase j by 1, note it down in lps array and then increase i by 1 to check the next character. j basically measures the longest chain of characters we were able to match. If we couldn’t match character at index i and if streak was greater than 0, then our new streak becomes whatever it was in the previous round of matching characters. If the streak is 0, then we simply note down at index i in our lps array 0, meaning longest length measured upto index i was 0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| public boolean repeatedSubstringPattern(String s) {
int maxLength = lps(s);
return maxLength > 0 && s.length() % (s.length() - maxLength) == 0;
}
private int lps(String s){
int len = s.length();
int[] lps = new int[len];
int i = 1; // To match the string with itself.
int j = 0;
while (i < len){
if (s.charAt(i) == s.charAt(j)){ // if the chars match
lps[i] = ++j; // we record that # of matches at index i was
++i; // 1+j and increment i to check next character
}
else{ // character did not match
if (j > 0) // If our matching streak > 0
j = lps[j-1]; // our new streak becomes the previous round's streak
else // Otherwise, streak is already 0.
lps[i++] = 0; // So we record that # of matches made at i is 0
} // We increment i to check next index.
}
return lps[len-1]; // Longest prefix length that was also a suffix
} // is whatever was recorded at the end of array.
|
The idea is simple. Count the number of cells with value 1 which denotes the land. Check towards the left and up to that cell and check if it shares any edge with another cell with value 1. If it does record that. In the end, the formula for perimeter is 4 * (the number of land cells) - 2 * (overlapping edges).
Reasoning: Perimeter of a square is 4 times the length of it’s side. Here all squares are of length 1. So total perimeter is 4*(number of cells with value = 1). But we also need to account the edges that are common between two adjacent land cells. If one square shares an edge with another, we just lost one side from both the square, resulting in a loss of two sides. Therefore, we need to subtract twice the number of overlapping edges from the total perimeter to get the total perimeter.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public int islandPerimeter(int[][] grid) {
int land = 0;
int overlap = 0;
for (int row = 0; row < grid.length; ++row)
for (int col = 0; col < grid[0].length; ++col){
if (grid[row][col] == 1){
++land;
if (row-1 > -1 && grid[row-1][col] == 1) // Check above the current cell.
++overlap; // If it's a land, we need to record one overlap.
if (col-1 > -1 && grid[row][col-1] == 1) // Similarly, check to the left.
++overlap; // If it's a land, we need to increment overlap
}
}
return 4*land - 2*overlap; // Check the reasoning above.
}
|
1
2
3
4
5
6
7
8
9
10
11
| public int findComplement(int num) {
int pow2 = 1; // Easily keep track of power of 2.
int comp = 0; // Complement number
while (num != 0){ // Since num gets divided by 2, it will be 0 in the end.
int bit = num % 2 == 0 ? 1 : 0; // If bit is 0 then complement is 1 & vice versa.
comp += bit * pow2; // Multiply it by the appropriate power of 2 and add to comp
pow2 *= 2; // Update power of 2 for next iteration.
num /= 2; // Divide num by 2 to get the next bit.
}
return comp; // Comp is now the complement.
}
|
The idea is as follows. We have 10 lights. First 4 represent hours. Namely 1, 2, 4 and 8, which are the first four powers of 2. The next 6 lights, represent minutes. Those are 1, 2, 4, 8, 16 and 32. These are powers of 2 from 0-5. So if we iterate from 1 to 9, powers of numbers 1-3 gives us hours and powers of numbers 4-9 minus 4 gives us minutes. So, if we have, let’s say 2 lights, we need to find every combination of 2 lights. So in our helper function, we iterate from 1-9 to check every hour and minute combination. We also need to keep a track of the lights that we used, so we don’t use the same light again. If hours are > 11 or minutes are > 59, we have an invalid time and we can abort. If the number of lights are 0, that means we found a valid time and we should add it to the result. Now, if the lights are not 0, then we need to check every possible combination from the last light used to 9. If i < 4, then we are looking at an hourly combination, otherwise it’s a minute combination. So we recurse with updated lights used, decrease the numOfLights since we used one, update respective hours or minutes until we hit base case.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| List<String> result;
public List<String> readBinaryWatch(int num) {
result = new ArrayList<>();
helper(0, num, 0, 0);
return result;
}
private void helper(int lightsUsed, int numOfLights, int hrs, int min){
if (hrs > 11 || min > 59) // Base case. Invalid time
return;
if (numOfLights == 0){ // All lights used, so add time to the list.
result.add(hrs + ":" + (min < 10 ? "0" + min : min));
return;
}
for (int i = lightsUsed; i < 10; i++){ // Otherwise start recursing from number of prev
if (i < 4) // light used. i < 4 means hours
helper(i+1, numOfLights-1, hrs + (int)Math.pow(2, i), min);
else // i = [4,9] means minute. So recurse.
helper(i+1, numOfLights-1, hrs, min + (int)Math.pow(2,i-4));
}
}
|
This was an interesting problem. But after working out a few examples by hand, you can notice that it is always a question of bringing the minimum element in par with everyone. So if you know the minimum of the array, we can check how many steps it will take to bring the minimum in par with other element by calculating the distance between them. For example,
Let the array be [1,2,3]
We can observe that the minimum here is 1. Let us list down all steps to make all elements equal.
- [2,2,4], Keeping the second element fixed. Notice that distance between the element where 1 was and where 3 was is till the same.
- [3,3,4], Keeping the last element fixed.
- [4,4,4], Keeping last element fixed.
Here, we first tried to make 1 equal to it’s neighbor, which required us 1 step. Now, once it becomes equal to 1, the problem is how to make the last element in the original array, which is 3 equal to 1. It requires 2 steps, resulting in a total of of 3. The reason is that the moment you decide to increment the minimum element to match the next element, you fix the neighboring element and have to increment everything else. This will make the minimum and its neighbor the same, but it will also keep the distance between the minimum and all other elements the same because we just incremented everything.
So, the total number of moves required is the distance between the elements of the array and the minimum.
1
2
3
4
5
6
7
8
9
10
| public int minMoves(int[] nums){
int min = nums[0];
for (int i: nums)
if (i < min)
min = i;
int moves = 0;
for (int i: nums)
moves += i-min;
return moves;
}
|
Now the above solution required two passes of the array. Can we do even better? Notice that in the end, all we are doing is finding the min and subtracting min from all the elements in the array. That means we are subtracting min n times where n is the length of the array. Why n times? Because there are n elements in the array. Shouldn’t it be (n-1) times? No, because the distance of the min from min is 0. So we need to subtract min from itself too, so n times. We can achieve this by first calculating the total of the array while simultaneously keeping track of the minimum. Once done, all we need to do is subtract min n times from the sum, which is equivalent to subtracting min from each element. This results in a much overall better algorithm, requiring only 1 pass of the array.
1
2
3
4
5
6
7
8
9
| public int minMoves(int[] nums) {
int sum = 0, min = nums[0];
for (int i: nums){
sum += i;
if (i < min)
min = i;
}
return sum - min*nums.length;
}
|
The idea is simple.
- I maintain a temporary array s that contains only the characters in string S after converting them to uppercase.
- I maintain a variable length that counts how many characters I found in the string S. If length is 0, that means it contains only dashes (-).
- Then I record the offset. Offset basically measures how many characters of the String S will be grouped unevenly in the beginning part of the string. I can check that by using the modulus operator and finding out the remainder. That many characters (of length < K) will be in the beginning part of the string.
- Next step is to calculate how many dashes I will need. It’s basically length / K.
- Then I create the char array that will hold the characters of the formatted key. It’s length will be number of characters + the dashes we will need. We need to take care of a special case here. If the offset is 0, meaning I was able to divide characters in equal group, I need to subtract 1. Eg, let’s say we had 8 characters and K was 4. dashes = 8 / 4 = 2. We can divide 8 characters equally into 2 groups using only 1 dash. But since dashes was 2, it is clearly off by 1. This is the case when offset is 0.
- kIndex tracks where character is to be inserted in the key array.
- used tracks how many characters of the array s, which indirectly holds the characters of String S, are used.
- First I copy down the characters of length offset. Because those are the ones of uneven length. kIndex and used variables are updated.
- Last thing to do is to use all the remaining characters in array s, but we take K characters at a time, because we know that the segments are going to be of equal length. We also need to insert ‘-’ after each segment, but only if kIndex is not at the beginning or at the end of the key array, because inserting it at those points is invalid.
- Create a new string and return it.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public String licenseKeyFormatting(String S, int K) {
char[] s = new char[S.length()];
int length = 0;
for (char c: S.toCharArray())
if (c != '-')
s[length++] = Character.toUpperCase(c);
if (length == 0)
return "";
int offset = length % K;
int dashes = length / K;
char[] key = new char[length + dashes + (offset == 0 ? -1 : 0)];
int kIndex = 0;
int used = 0;
while (used < offset)
key[kIndex++] = s[used++];
while (used < index){
if (kIndex > 0 && kIndex < key.length)
key[kIndex++] = '-';
for (int i = 0; i < K; ++i)
key[kIndex++] = s[used++];
}
return new String(key);
}
|
Solution 1: I came up with this solution initially. 4 ms runtime and passes 99.97% submissions.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public int findMaxConsecutiveOnes(int[] nums) {
int start = 0; // Keep track of start of a streak, if any
int max = 0; // max length of the streak
while (start < nums.length){ // While we are not at the end of the array
if (nums[start] == 1){ // Check if we have a 1 at start, if so
int streak = 0; // initialize streak and check how long can we continue
while (start < nums.length && nums[start] == 1){ // that streak.
++streak; // Increment streak and left for each consecutive 1
++start; // make sure you don't forget that start < nums.length
} // before checking nums[start] to prevent out-of-bounds
if (streak > max) // Check if the current streak is better than the
max = streak; // previous streak.
}
++start; // Increment start in either case to check for new
} // streaks.
return max;
}
|
Solution 2: After analyzing the problem further, I noticed that 0 denotes the end of a streak. If we observe 1, we increment streak by 1. But if I see a 0, I reset my streak to 0. This solution too had a 4 ms runtime and passed 99.97% submissions.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public int findMaxConsecutiveOnes(int[] nums) {
int max = 0; // Global max streak
int streak = 0; // Local max streak.
for (int i: nums){ // For each number in nums
if (i == 1){ // If we see a 1
++streak; // increment our ongoing streak.
if (streak > max) // If the local streak > global max
max = streak; // update global max streak.
}
else // otherwise we just saw a 0.
streak = 0; // So our streak resets to 0.
}
return max; // return the global max streak.
}
|
The idea is as follows. Given an array a = {1,2,3}, we want to generate all it’s possible combinations. What we are trying to do here is that we first take the element at index 0, and find permutations of the remaining thing. When we do that, we insert the element at index 0 in front of the list to get 1 permutation. Similarly, we then take the element at index 1, and permute the remaining contents of the array and insert the element at index 1 in the beginning of the array to get another permutation and so on. In this problem, we are asked to return a list of list, so we first copy the numbers of the array into an ArrayList. Let’s run this code for the above example.
Given nums = {1,2,3}, our ArrayList will be the same, al = [1,2,3]. Our result list is empty, result = [] and index = 0.
helper([1,2,3], 0)
swap (0, 0) → al = [1,2,3]
helper(1,2,3, 1)
swap(1, 1) → al = [1,2,3]
helper([1,2,3], 2)
swap(2, 2) → [1,2,3]
helper([1,2,3], 3)
We update our result list now, because index == length. Therefore, result = [[1,2,3]]. Our recursive stack collapses and we move on to the next instruction, which is undo the step, al = [1,2,3].
swap(1, 2) → al = [1,3,2]
helper([1,3,2], 3)
Again, index == length, add it to the list. result = [[1,2,3], [1,3,2]]. Recursion stack collapses, we undo the swap, al = [1,2,3]
swap(0, 1) → al = [2,1,3]
helper([2,1,3], 1)
swap(1,1) → al = [2,1,3]
helper([2,1,3], 2)
swap(2, 2) → al = [2,1,3]
helper([2,1,3], 3)
index == length, add the current order to the list. result = [[1,2,3], [1,3,2], [2,1,3]]
swap(1, 2) → al = [2,3,1]
helper([2,3,1], 3)
index == length, add the order to the list. Result = [[1,2,3], [1,3,2], [2,1,3], [2,3,1]]
swap(0, 2) → al = [3,2,1]
helper([3,2,1], 2)
swap(2,2) → al = [3,2,1]
helper([3,2,1], 3)
index == length, add the order to the list. Result = [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,2,1]]
swap(1,2) → al = [3,1,2]
helper([3,1,2], 3)
index == length, add the order to the list. Result = [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,2,1], [3,1,2]]
All branches have been explored now, since the iteration ends and we return the result list.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| int len; // To store the length of the input array
List<List<Integer>> result; // Result list
public List<List<Integer>> permute(int[] nums) {
result = new ArrayList<>();
List<Integer> numList = new ArrayList<>(); // Creating a copy of the nums array
for (int i: nums) // because it's easier to create a list from a list.
numList.add(i); // Add everything to the list.
len = nums.length;
helper(numList, 0); // Call the aux function.
return result;
}
private void helper(List<Integer> order, int index){
if (index == len) // If we have checked all the numbers in the array, add a
result.add(new ArrayList<>(order)); // clone of the list to the array.
for (int i = index; i < len; ++i){ // Otherwise from index to the end of the array,
swap(order, i, index); // take one element, swap it with itself, then the next and
helper(order, index+1); // so on. Recurse again, but on the next index we just swapped.
swap(order, i, index); // Undo the swap so that it helps us in generating the next
} // permutation.
}
private void swap(List<Integer> list, int i, int j){ // Swap elements in a list.
int temp = list.get(i);
list.set(i, list.get(j));
list.set(j, temp);
}
|
The idea is very simple. We just need to iterate from width = sqrt(area) to 1 and check if area is perfectly divisible by width. If at any point, width is divisible, then that must be our minimum difference length and width, because we are diverging from the center on both sides. Width decreases while length keeps increasing. Think of it like this, for area = 24, we have many factors of 24, namely 1, 2, 3,4, 6, 8, 12, 24. It’s sqrt when rounded down is 4. So we check for width = 4, is 24 perfectly divisible by 4? Yes, so divide it and whatever you get is going to be the minimal difference values. Suppose 4 and 6 weren’t the factors for 24. In that case we decrease width by 1, which is 3. Check again, is 24 divisible by 3. Yes? Then that must be our answer. We are diverging away from the center on both sides equally, width to the left towards 1 and length to the right towards area . Therefore the moment we find one value that divides area perfectly, that’s our required values.
1
2
3
4
5
6
7
8
9
10
11
12
13
| public int[] constructRectangle(int area) {
int[] dimensions = {area, 1}; // We know that if nothing works out, n*1 is always
boolean done = false; // going to be the answer
int width = (int)Math.sqrt(area); // We only need to check width from sqrt(area)
while (!done){ // While not done
if (area % length == 0){ // check if area is perfectly divisible by width
dimensions[0] = width; // if so, we found our width and the length.
dimensions[1] = area/width;
done = true; // mark done as false
}
--width; // otherwise decrease the length
}
return dimensions; // return the dimensions found.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public List<Interval> merge(List<Interval> intervals) {
if (intervals == null || intervals.size() < 2)
return intervals;
Collections.sort(intervals, (a,b) -> a.start-b.start); // Sort the list so we can
// compare adjacent intervals.
List<Interval> merged = new ArrayList<>();
merged.add(intervals.get(0)); // Add the initial interval.
for (Interval i: intervals){ // For each interval
Interval last = merged.get(merged.size()-1);// Get the last added time.
if (i.start > last.end) // If it's time is greater than the last
merged.add(i); // interval's end, it doesn't overlap
else{ // otherwise it does.
last.end = last.end > i.end ? last.end : i.end; // So check which has greater end time, and make the last added interval's time equals that
merged.set(merged.size()-1, last); // And set it as the last added interval
}
}
return merged; // Return the merged list.
}
|
- counterA keeps track of which element we are looking at in array ‘a’. Same with counterB
- counterK keeps track of where to insert the element in array ‘a’, since a has enough space. The problem states that it might have more than enough space, so we use only the spaces we need, which is the total of both their sizes. Since indexing in an array is 0-based, we subtract 1.
- We insert elements from the end, since the end part of ‘a’ is empty. We can insert from the front, but then we would need to shift elements to the right after each insertion from ‘b’.
- If array values are equal, add them to the end, and decrease both their counter to check new values in the next iteration
- If not equal, then check which one is greater, since the last part of the array should contain larger values. Whichever’s greater, put it in ‘a’ at index ‘counterA’ and decrement the respective counter.
- In the end, we might have some leftover elements either from ‘a’ or ‘b’ because we only process elements that are equal to the min(size(a), size(b)), until we run out of elements in one of the array. So, whichever array has elements pending, add it to the front of the array and return a.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public int[] merge(int[] a, int sizeA, int[] b, int sizeB)
{
int counterA = sizeA-1, counterB = sizeB-1, counterK = sizeA+sizeB-1;
while (counterA > -1 && counterB > -1){
if (a[counterA] == b[counterB]){
a[counterK--] = a[counterA--];
a[counterK--] = b[counterB--];
}
else
a[counterK--] = a[counterA] > b[counterB] ? a[counterA--] : b[counterB--];
}
while (counterA > -1)
a[counterK--] = a[counterA--];
while (counterB > -1)
a[counterK--] = b[counterB--];
return a;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public int[] nextGreaterElement(int[] nums1, int[] nums2) {
HashMap<Integer, Integer> index = new HashMap<>(); // We use the hashmap to keep a
for (int i = 0; i < nums2.length; ++i) // track of the index of each value
index.put(nums2[i], i); // in nums 2. That way, when we want
// to look for a value greater than a val in nums1, we know
int[] result = new int[nums1.length]; // which index to start iterating from.
for (int i = 0; i < nums1.length; ++i){ // So for each val in nums1
int val = nums1[i];
for (int j = index.get(val); j < nums2.length; ++j){ // Iterate from that value's
if (nums2[j] > val){ // index in nums2 to the end, and see if you can
result[i] = nums2[j]; // find any val > nums1[i]. If you do, save it
break; // in the result array and break the loop.
}
}
if (result[i] == 0) // Now if we didn't find any value, then result[i] would be
result[i] = -1; // 0, so we set that index to -1 in our result array.
}
return result; // simply return the result array.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| public String strWithout3a3b(int A, int B) {
char[] ch = new char[A+B]; // We create an char array to store string chars
int index = 0;
char max = A > B ? 'a' : 'b'; // record the most frequent occurring element
char min = max == 'a' ? 'b' : 'a'; // and the least frequent occurring element
while (A > 0 || B > 0){ // While we haven't added all of the elements
// We check that if our current index > 1 and our previoud two characters in the array
// are the same, then we must have written the max occurring char, so it's time to write
// the minimum occurring element. We write it, and then decrement the specific A or B.
if (index > 1 && max == ch[index-1] && max == ch[index-2]){
ch[index++] = min;
if (min == 'a') // If the minimum freq element is 'a', decrement A
A--;
else
B--; // otherwise decrement B
}
else if (B > A){ // Otherwise, if B occurs more than A, then set char to B
ch[index++] = 'b'; // decrement B and increment index
B--;
}
else{ // A occurs more, so add A to the char array.
ch[index++] = 'a'; // Increment index, decrement A count
A--;
}
}
return new String(ch); // Create a string from the char array and return it.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| // Maps each character to the row in the keyboard in which it occurs.
private int[] map = {2,3,3,2,1,2,2,2,1,2,2,2,3,3,1,1,1,1,2,1,1,3,1,3,1,3};
public String[] findWords(String[] words) {
String[] w = new String[words.length]; // Store filtered words
int index = 0; // Where to insert the filtered words
for (String s: words) // for each word in words
if (checkWord(s.toLowerCase())) // convert it to lowercase and check if all char
w[index++] = s; // occurs in the same row, if it does, add it
return Arrays.copyOfRange(w, 0, index); // Simply return a copy of the array from 0
} // index
private boolean checkWord(String word){ // Check if all chars in the word belong in the
int row = map[word.charAt(0)-'a']; // same row. Check first chars row
for (char c: word.toCharArray()){ // For all the chars in the word
if (map[c-'a'] != row) // if that char belongs to a different row,
return false; // return false
}
return true; // All chars in same row, return true.
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| private TreeNode parent; // Keep track of parent at each node
private int maxMode; // maxMode we found
private int currentMode; // mode recorded at each node
private Set<Integer> modes; // keep distinct modes found
public int[] findMode(TreeNode root){
if (root == null) // node is null, so return empty array
return new int[0];
maxMode = 1; // we have just seen the root, so maxMode so far is 1.
currentMode = 1; // so is the current mode
modes = new HashSet<>();
modes.add(root.val); // add the root to our modes set
traverse(root); // start traversing it's left and right branches
int[] result = new int[modes.size()]; // We have found all the modes
int idx = 0; // keep track of where to insert elements in result array
for (int i: modes) // add all the distinct modes one by one
result[idx++] = i;
return result; // and return it.
}
private void traverse(TreeNode node){
if (node == null) // if node is null, stop
return; // otherwise traverse the left branch
traverse(node.left); // Once we hit the null, we start backtracking to the leaf
updateMode(node); // then we call updateMode with the node
parent = node; // once it's done, we update parent as the current node, so
traverse(node.right); // when we backtrack, we can easily check that node and it's
} // next node's value for similarity. Then traverse right.
private void updateMode(TreeNode node){
if (parent != null && parent.val == node.val){ // If parent node isn't null and the
++currentMode; // node's value is the same as parent, we update currentMode
if (currentMode >= maxMode){ // If the currentMode is greater or equal to maxMode
if (currentMode > maxMode) // just check if it's greater. If it is, remove all
modes.clear(); // previously recorded modes
modes.add(node.val); // Add the current node to the set and update the
maxMode = currentMode; // maxMode
}
}
else{ // otherwise, value's aren't the same. so our currentMode
currentMode = 1; // becomes 1. If maxMode is also 1, then all we have been
if (maxMode == 1) // seeing are distinct values, so add that node's value to
modes.add(node.val);// to the mode's set.
}
}
|
Solution 1 without StringBuilder (Beats 100%, 7ms)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public String convertToBase7(int num) {
if (num == 0)
return "0";
int len = (int)(Math.log(Math.abs(num))/Math.log(7))+1; // Calculate # of bits
int idx; // where to start inserting from
char[] digits;
if (num < 0) { // If num is negative
num = -num; // Make it positive
digits = new char[len+1]; // We need one more space for -ve sign in the front
digits[0] = '-'; // Put the -ve sign
idx = len; // and index is now len
}
else{
digits = new char[len]; // otherwise we only need "len" spaces
idx = len-1; // index is len-1
}
while (num != 0) { // While num != 0, calculate remainder and add it.
digits[idx--] = (char)(num % 7 + '0'); // Divide number by 7
num /= 7;
}
return new String(digits); // Just create a string and return it.
}
|
Solution 2 with StringBuilder
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public String convertToBase7(int num) {
StringBuilder sb = new StringBuilder();
boolean isNegative = num < 0; // Just so we can know if we need to add the "-" sign
if (num < 0) // Take the absolute value of num
num = -num;
while (num > 6) { // Keep adding the remainder, and dividing num by 7.
sb.append(num % 7);
num /= 7;
}
sb.append(num); // Add whatever is left at the end.
if (isNegative) // If num was negative, add the minus sign.
sb.append('-');
return sb.reverse().toString(); // Reverse the builder and return the toString()
}
|
The idea employed here is simple. We need to store the relative ranks in sorted order. We can sort the array for that, but that is O(n log n). We can do better than that by finding the relative rank in linear time. First we find the maximum score in the array and create another array of length = maxScore + 1. We add 1 so that when we see the maxScore in the nums, we can assign it to maxScore index. Once we have done that, now we iterate over the nums array. Variable i keeps track of what rank to assign. We check a value in the array and at that index in our reverse sorted array, we put i+1, which basically marks it’s rank based on it’s position in the rankings. Some of then indexes would be default, that is a score of 0. We then check each value in the descend array and if it’s not 0, we assign it a rank, but not if the ranks are 1, 2 or 3. In that case, we assign it a special value of Gold, SIlver or Bronze.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public String[] findRelativeRanks(int[] nums) {
int maxScore = nums[0];
for (int n: nums)
if (n > maxScore)
maxScore = n;
int[] descend = new int[maxScore+1];
for (int i = 0; i < nums.length; ++i)
descend[nums[i]] = i+1;
String[] result = new String[nums.length];
int rank = 1;
for (int i = descend.length-1; i > -1; --i){
int idx = descend[i];
if (descend[i] != 0){
if (rank == 1)
result[idx-1] = "Gold Medal";
else if (rank == 2)
result[idx-1] = "Silver Medal";
else if (rank == 3)
result[idx-1] = "Bronze Medal";
else
result[idx-1] = rank + "";
++rank;
}
}
return result;
}
|
1
2
3
4
5
6
7
8
9
10
11
| public boolean checkPerfectNumber(int num) {
if (num == 1) // 1 is a special case, where it's only factor is itself.
return false;
int total = 1; // We know our total will atleast be 1, 1 is everyone's factor
for (int i = 2; i <= Math.sqrt(num); ++i) // Only loop through num's sqrt
if (num % i == 0){ // If i divides num perfectly
int otherFactor = num/i; // Calculate the other factor
total += i + (otherFactor == i ? 0 : otherFactor); // If i and other factor are
} // different, add them both, otherwise just i.
return total == num; // Check in the end if your total is the same as num
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public boolean detectCapitalUse(String word) {
int len = word.length();
if (len < 2) // Empty or size 1 words are ok.
return true;
char[] chars = word.toCharArray(); // Get the char array
boolean isUpper = false; // by default we let isUpper to false
if (chars[0] >= 'A' && chars[0] <= 'Z') // Check if first two letters are uppercase
isUpper = chars[1] >= 'A' && chars[1] <= 'Z'; // If first was upper and second wasnt
for (int i = 1; i < len; ++i){ // isUpper = false, otherwise true.
boolean isAlsoUpper = chars[i] >= 'A' && chars[i] <= 'Z'; // We check onwards 1 char
if (isUpper && !isAlsoUpper) // If that char is lower and previous part was
return false; // not lower, invalid use.
if (!isUpper && isAlsoUpper) // Or if previous part was lower and current letter
return false; // is upper, we return false.
}
return true; // Everything proceeded smoothly. So return true.
}
|
This is those kind of problems that shouldn’t be up there. The problem is stated rather poorly and the solution is even stupider. All you are checking for is if the two string’s aren’t the same, then whichever one has a larger length is essentially the longest uncommon subsequence because the other string cannot form the full string. I know, it’s stupid.
1
2
3
4
5
| public int findLUSlength(String a, String b) {
if (a.equals(b))
return -1;
return a.length() > b.length() ? a.length() : b.length();
}
|
This is a graph problem where we require to sort the vertices topologically. There are two choices we have for sorting topologically - Depth First Search approach based on finshing times or the Kahn’s Algorithm. I have used Kahn’s algorithm in this solution. Runtime is 2ms [beats 100%] and uses 45.3 MB space [beats than 90.16%]. The idea for Kahn’s is simple - Enqueue all the nodes which has 0 incoming edges because those are the ones that can be started first. Then while the queue isn’t empty, remove one node at a time, process it’s outgoing nodes and decrease their indegrees by one. The reasoning behind that is let’s say Node 2 has two prerequisites, Node 0 and Node 1. Node 0 and Node 1 have 0 indegrees. So our first two nodes would be Node 1 and Node 0 and if they are finished, then their outgoing Nodes can be started, that is Node 2. Now when you decrease any node’s indegree and they become zero, add them to the queue because they can now be started. Keep doing this until the queue is empty.
In my approach, I’m avoiding any unnecessary data structure and using only the most basic ones like array’s. So instead of using the queue, what I do is fill the array order which also stores the topological order. idx keeps track of the last index available to fill in the array. start mimics the poll behaviour of a queue. while (start != idx) makes sure that while we still have nodes to process, remove the one that can be started and decrease all the indegrees of outgoing edges.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public int[] findOrder(int numCourses, int[][] prerequisites) {
int[] indegrees = new int[numCourses]; // We maintain each node's indegree
List<Integer>[] graph = new ArrayList[numCourses]; // Each node's outgoing edges
for (int[] edge: prerequisites) { // Process each edge
indegrees[edge[0]]++; // Update indegrees
if (graph[edge[1]] == null) // Also store the edge in graph
graph[edge[1]] = new ArrayList<Integer>();
graph[edge[1]].add(edge[0]);
}
int[] order = new int[numCourses]; // We don't technically need a queue.
int idx = 0;
for (int i = 0; i < numCourses; ++i) // Find all nodes who indegree is 0
if (indegrees[i] == 0) // and put them in the order array
order[idx++] = i;
int start = 0; // start tracks node to be polled.
while (start != idx) { // while we can poll the queue
int u = order[start++]; // poll the node u
if (graph[u] != null) // If node u has outgoing edges
for (int out: graph[u]) // Then for each of those nodes
if (--indegrees[out] == 0) // decrease their indegrees and check if it's 0
order[idx++] = out; // if it's 0, add it to our queue (order)
}
if (idx != numCourses) // Cycle check. If our idx != numCourses then
return new int[] {}; // not all nodes could be processed. So we have
return order; // a cycle. Otherwise return our order array.
}
|
Runtime: 0 ms, faster than 100.00% of Java online submissions for Letter Combinations of a Phone Number.
Memory Usage: 35.9 MB, less than 98.63% of Java online submissions for Letter Combinations of a Phone Number.
How do we count numbers? 16, 17, 18, 19 and then what? 20 right? We see that the last number is 19, we can’t go past 9 so we set it to 0 and then increment the precedding digit to get 20. The idea is the same for this problem too. We keep a levels array to keep track of which character do we take from which number’s allowed alphabet letters. For example, let’s say the input string is 23. Our levels array would [0, 0] in the beginning. This says pick characters at index 0 and 0 from alphabet characters corresponding to 2 and 3 which gives us ad. Then, we increase the last most counter in our levels array by 1 giving us [0, 1]. This allows us to get ae in the next iteration and levels array would be [0, 2]. We get af and levels array becomes [0, 3]. Now this is where it becomes interesting. We are only allowed three letters for the digit corresponding to 3 and since we already used all of them , we now need to shift to the next character for digit 2, which is b. Level array looks like [1, 0]. This will allow us to get [b,e]. So you get the rough idea now. Only thing now is we watch out when to stop. We stop when we have utilized all available characters from the 0th index’s number’s allowed alphabet letters. In this case, we stop when levels array look like [3, 0].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| class Solution {
private char[][] map = {
{'a', 'b', 'c'}, // 2
{'d', 'e', 'f'}, // 3
{'g', 'h', 'i'}, // 4
{'j', 'k', 'l'}, // 5
{'m', 'n', 'o'}, // 6
{'p', 'q', 'r', 's'}, // 7
{'t', 'u', 'v'}, // 8
{'w', 'x', 'y', 'z'} // 9
};
private List<String> result = new ArrayList<>(); // Maintain the list of combinations
private int[] numbers; // numbers parsed from input
private int[] levels; // utility array to keep track of next character in string
private int n; // number of input digits.
private List<String> solution(String digits) {
if (digits == null || digits.length() == 0) // stop if null or empty string
return result;
n = digits.length();
numbers = new int[n];
levels = new int[n];
for (int i = 0; i < digits.length(); ++i) { // parse all the digits from the string as int
if ((numbers[i] = digits.charAt(i) - '0') < 2) // stop if any of them is 0 or 1
return result;
}
helper(); // start recursion
return result;
}
private void helper() {
if (levels[0] == map[numbers[0]-2].length) // if we are done iterating over all possible combinations,
return; // stop recursion.
char[] s = new char[n]; // stores all the characters of the string
for (int i = 0; i < n; ++i) // loop through levels array. The value at each index
s[i] = map[numbers[i]-2][levels[i]]; // tells us which character to keep from which map index
levels[n-1]++; // Increase the entry at the end of the levels array
for (int i = levels.length-1; i > 0; --i) { // Now loop through the levels array from the end
if (levels[i] == map[numbers[i]-2].length) { // If the value = total number of characters allowed for that number
levels[i] = 0; // then we set it to 0 and increment the previous level entry
levels[i - 1]++;
}
}
result.add(new String(s)); // Add the string and induce next recursive call.
helper();
}
}
|
Runtime: 4 ms, faster than 90.01% of Java online submissions for Sudoku Solver.
Memory Usage: 35.1 MB, less than 71.93% of Java online submissions for Sudoku Solver.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| private char[][] board;
public void solveSudoku(char[][] board) {
this.board = board;
solve(0, 0);
}
private boolean solve(int row, int col) {
if (col == 9) { // If col is 9, make it 0 and shift to the next row
col = 0;
row += 1;
if (row == 9) // If row is also 9 now, then it means we have successfully filled all cells
return true; // So return true and end backtracking.
}
for (int i = 1; i < 10; ++i) { // Otherwise, we start picking values from 1-9
if (board[row][col] == '.') { // And try to plug it into empty cells
if (isValid(row, col, i)) { // If that value is valid in that cell
board[row][col] = (char)(i+'0'); // fill it
if (solve(row, col+1)) // and move on to fill the next cell via recursive call
return true; // If the recursion ended by returning true, then return true to signal success
else // Otherwise, we were not able to put an value in that cell
board[row][col] = '.'; // so change it back to 0 and the backtracking would try the next higher value in that cell.
}
}
else
return solve(row, col+1); // That cell wasn't empty, so move on to the next empty cell.
}
return false; // No solution found.
}
private boolean isValid(int row, int col, int val) {
// row check
for (int c = 0; c < 9; ++c)
if (board[row][c] - '0' == val)
return false;
// column check
for (int r = 0; r < 9; ++r)
if (board[r][col] - '0' == val)
return false;
// box check
int top = row / 3 * 3;
int left = col / 3 * 3;
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
if (board[top+i][left+j] - '0' == val)
return false;
}
}
return true;
}
|
Runtime: 1 ms, faster than 100.00% of Java online submissions for Bulls and Cows.
Memory Usage: 36.3 MB, less than 100.00% of Java online submissions for Bulls and Cows.
The idea is simple, first record the frequency of the digits of the secret number. Then we first find number of bulls by checking for exact indices match. After that we start to record the number of cows. The way we do is by again iterating over the guess string; only if there was a character mismatch and we still have the character available from freq table, we have a cow. Update it and decrement the frequency of the number we just used up.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| public String getHint(String secret, String guess) {
int bulls = 0;
int cows = 0;
int[] freq = new int[10]; // Freq of available digits from secret
for (int i = 0; i < guess.length(); ++i) {
char s = secret.charAt(i);
freq[s - '0']++; // Record the freq of the digit
if (s == guess.charAt(i)) { // If it's a match, we have a bulls.
bulls++;
freq[s - '0']--; // We just used the character, so decrement it.
}
}
for (int i = 0; i < guess.length(); ++i) {
int s = secret.charAt(i) - '0'; // Convert the chars into int
int g = guess.charAt(i) - '0';
if (s != g && freq[g] > 0) { // Only if they are a mismtach and we have a number g available in freq table
cows++; // then it's a cow.
freq[g]--; // We used up the number, so decrement it's freq.
}
}
return new StringBuilder().append(bulls).append("A").append(cows).append("B").toString();
}
|
Runtime: 3 ms, faster than 73.76% of Java online submissions for N-Queens.
Memory Usage: 37.6 MB, less than 100.00% of Java online submissions for N-Queens.
The idea is same as sudoku, but insteading of scanning rows, we scan columns. Start with row 0, column 0 and see if we can place a queen there, if yes place it and try the next cell of row 0 by recursing. We can’t put the queen in the same row again, so we keep changing rows with column 1 until we find somewhere to place it. Keep doing this until you were successfully able to place all the queens as checked by the condition col == n. If so, add that solution to our list of accepted solutions.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| public class NQueens {
private int[][] board;
private int n;
private List<List<String>> result;
public List<List<String>> solveNQueens(int n) {
this.n = n;
board = new int[n][n];
result = new ArrayList<>();
solve(0);
return result;
}
private boolean solve(int col) {
if (col == n)
addToList();
for (int row = 0; row < n; ++row) {
if (canPlaceQueen(row, col)) {
board[row][col] = 1;
if (solve(col+1)) {
return true;
}
else
board[row][col] = 0;
}
}
return false;
}
private void addToList() {
List<String> list = new LinkedList<>();
StringBuilder sb;
for (int[] r: board) {
sb = new StringBuilder();
for (int i: r)
sb.append(i == 1 ? 'Q' : '.');
list.add(sb.toString());
}
result.add(list);
}
private boolean canPlaceQueen(int row, int col) {
// Check all rows for the same column
for (int i = 0; i < col; ++i) {
if (board[row][i] == 1)
return false;
}
// Check upper left diagonal of the cell
for (int i = row, j = col; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 1)
return false;
}
// Check lower left diagonal of the cell.
for (int i = row, j = col; i < n && j >= 0; i++, j--) {
if (board[i][j] == 1)
return false;
}
return true;
}
}
|
Pretty intuitive solution. Build a frequency HashMap for all the numbers in the array. In a special case where diff is 0, just count occurences in our freq map whose values are 2 or more. In other case, just loop through all the keys and make sure it’s supplement exists to count the number of K-diff pairs.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public int findPairs(int[] nums, int k) {
if (k < 0)
return 0;
int pairs = 0;
HashMap<Integer, Integer> freq = new HashMap<>();
for (int i: nums) {
freq.put(i, freq.getOrDefault(i, 0)+1);
}
if (k == 0) {
for (int i: freq.values())
if (i > 1)
pairs++;
return pairs;
}
for (int i: freq.keySet()) {
if (freq.containsKey(i+k))
pairs++;
}
return pairs;
}
|
Runtime: 0 ms, faster than 100.00% of Java online submissions for Is Subsequence.
Memory Usage: 49.6 MB, less than 100.00% of Java online submissions for Is Subsequence.
1
2
3
4
5
6
7
8
9
| public boolean isSubsequence(String s, String t) {
int idx = -1; // Set it to 0 to start check for 0th index
for (char c: s.toCharArray()) { // For all the characters in String s
idx = t.indexOf(c, idx+1); // Find it's index in String t from index one more than the last index matched
if (idx < 0) // idx < 0 means not found
return false;
}
return true;
}
|
The idea is to use the Inorder traversal of a BST. We repeatively iterate over the left branch to find the minimum diff and then do the same for the right branch, but this time we already know that the parent of the right branch has to be its minimum, so first set it and then traverse the right branch to find the minimum difference.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| int res = Integer.MAX_VALUE; // Hold the minimum difference.
int prev = Integer.MAX_VALUE; // Holds the minimum value observed for the right branch
public int getMinimumDifference(TreeNode root) {
traverse(root); // Start iterating from the root.
return res;
}
private void traverse(TreeNode node) {
if (node == null) // Null node, so stop recursion
return;
traverse(node.left); // Keep traversing till the end of the tree
res = Math.min(Math.abs(node.val-prev), res); // Check if we have a minimum, if so set it.
prev = node.val; // The smallest value for the right branch is it's parent
traverse(node.right); // Set it first and then traverse.
}
|
The idea is simple. In a BST, we know everything on the right side of a node is greater than it and it’s left side. So when we are at any node, it’s value would be its value + sum of everything on its right side. So, we first compute the node’s value and then notice that the value for the node on the left is nothing but its value + parents value. So the node’s value is computed, do the same thing for the left side, but this time, the starting sum would be the parent’s value.
1
2
3
4
5
6
7
8
9
10
11
| public TreeNode convertBST(TreeNode root) {
traverse(root, 0);
return root;
}
private int traverse(TreeNode node, int sum) {
if (node == null)
return sum;
node.val += traverse(node.right, sum);
return traverse(node.left, node.val);
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public boolean checkRecord(String s) {
int A = 0; // Count number of A's seen
int L = 0; // Count number of consecutive L's seen
for (char c: s.toCharArray()) { // Loop through each character
if (c == 'A') { // If c is A, increment A
A++;
if (A > 1) // If A is more than 1, return false
return false
L = 0; // Always set L count to 0
}
else if (c == 'L') { // If c is L,
L++; // We might have consecutive L's, so start counting
if (L > 2) { // If we have more than 2 consecutive L's
return false; // return false
}
}
else // Lastly, we might have a P, that will reset our
L = 0; // consecutive L streak.
}
return true; // Everything passed, so return true.
}
|
Runtime: 2 ms, faster than 99.34% of Java online submissions for Reverse Words in a String III.
Memory Usage: 37.9 MB, less than 100.00% of Java online submissions for Reverse Words in a String III.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public String reverseWords(String s) {
char[] arr = s.toCharArray();
int len = arr.length;
int start = 0;
int end;
while (start < len) { // Check the whole string
end = start; // find the index of the first whitespace
while(end < len && arr[end] != ' ') // denoting end of the word
end++;
reverseWord(arr, start, end-1); // reverse that specific word
start = end+1; // update start to the new word beginning
}
return new String(arr); // create a new string out of the array
}
/*
Reverses a word in-place by iterating n/2 times where n = len of the word.
Traverse upto the middle point of the word while swapping each word from start+offset to end- offset.
**/
private void reverseWord(char[] arr, int start, int stop) {
for (int i = 0; i <= (stop-start)/2; ++i) {
char temp = arr[start+i];
arr[start+i] = arr[stop-i];
arr[stop-i] = temp;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public Node intersect(Node qt1, Node qt2) {
if (qt1.isLeaf) // If only a leaf, then return the one with true val
return qt1.val ? qt1 : qt2;
if (qt2.isLeaf)
return qt2.val ? qt2 : qt1;
Node n = new Node(); // Prepare for recursion
n.val = true; // By default, each level node is not a leaf with
n.isLeaf = false; // value = true
// Keep traversing all the way to a terminal node and then store it.
n.topLeft = intersect(qt1.topLeft, qt2.topLeft);
n.topRight = intersect(qt1.topRight, qt2.topRight);
n.bottomLeft = intersect(qt1.bottomLeft, qt2.bottomLeft);
n.bottomRight = intersect(qt1.bottomRight, qt2.bottomRight);
// Check now if you're at the base case. If n's children are leaves and all their values are same, then make n a leaf and it's value the same as it's child.
if (n.topLeft.isLeaf && n.topRight.isLeaf && n.bottomLeft.isLeaf && n.bottomRight.isLeaf && (n.topLeft.val == n.topRight.val && n.topRight.val == n.bottomLeft.val && n.bottomLeft.val == n.bottomRight.val)) {
n.isLeaf = true;
n.val = n.topLeft.val;
}
return n;
}
|
Runtime: 0 ms, faster than 100.00% of Java online submissions for Long Pressed Name.
Memory Usage: 34.2 MB, less than 100.00% of Java online submissions for Long Pressed Name.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public boolean isLongPressedName(String name, String typed) {
char[] n = name.toCharArray(); // Arrays are much nicer to work with
char[] t = typed.toCharArray(); // Record start and stop points for both
int startN = 0, endN = n.length, startT = 0, endT = t.length;
while (startT < endT) { // While we haven't looked at the whole string
int temp = startN+1; // Let's first count same consecutive letters
int countN = 1; // in String name
while (temp < endN && n[startN] == n[temp]) {
temp++;
countN++;
}
int countT = 0; // Do the same for typed string
while (startT < endT && n[startN] == t[startT]) {
startT++;
countT++;
} // If consecutive letters in typed string are
if (countT < countN) // less than the ones in original name
return false; // return false
startN = temp; // Otherwise, prepare for next character
}
return startN == endN; // Lastly, check if we were able to match
} // all character of the name string
|
The idea here is simple. We perform a BFS as usual using a Queue but I maintain a variable called dir to check which side do I add from. dir=1 means add from Right->Left and dir=-1 means add from usual Left->Right. I am also using LinkedList because of easy addition of elements in both direction. When I need to add from Right->Left, I use the addFirst(E e) method of LinkedList to add to the head, otherwise normal add to the tail. One important thing to take care of at each iteration is to know how many nodes to dequeue, hence the usage of the variable children. This allows me to keep track of how many children were added to the queue at each stage so I dequeue exactly that many children in the next stage. Apart from that, everything is straightforward.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> list = new LinkedList<>();
if (root == null)
return list;
Queue<TreeNode> q = new LinkedList<>();
q.add(root); // Children = 1 because only root is added.
int dir = 1, children = 1; // Added the root, so next time dir = 1 (Right->Left)
while(!q.isEmpty()) {
int pushed = 0;
LinkedList<Integer> l = new LinkedList<>();
for (int i = 0; i < children; ++i) { // Poll only those nodes that were queued in
TreeNode u = q.poll(); // the previous stage.
if (dir == 1)
l.add(u.val);
else
l.addFirst(u.val); // Left->Right add
if (u.left != null) { // Add children, notice I am counting here
q.add(u.left); // how many children I am pushing/queuing
++pushed; // to the queue
}
if (u.right != null) { // Same thing for right child.
q.add(u.right);
++pushed;
}
}
list.add(l); // Add this list to main list
children = pushed; // update # of children pushed
dir = dir == 1 ? -1: 1; // update dir for next iteration
}
return list;
}
|
Runtime: 3 ms, faster than 99.90% of Java online submissions for Array Partition I.
Memory Usage: 40.1 MB, less than 100.00% of Java online submissions for Array Partition I.
I originally came up with the sorting solution where you sort the array and look at two numbers at a time and keep the smaller number out of them and add to the sum. It was way slower, so I checked the fastest submission and this one is pretty smart. The idea is really good. We know there are going to be 20,001 numbers, so reserve an array for it. Now let’s say we had duplicates in our array, ex [1,2,1,4,1,1], if we were to sort it, we would get [1,1,1,1,2,4]. Notice that those four 1’s don’t really matter because each of them pairs up with the other to give you a one 1. That is why we mark those particular indices as true and false. Notice that in our variable sum we would have counted them individually, making sum = 4 when in fact it should be 2 since we only take one of them from two pairs. If we have even occurrence of any number, they would be false, meaning we don’t need to account them in the diff calculation. Now coming to diff how do we compute it? First we have the seen array to know which elements we need to look at. If that particular index is true, then we check if it’s the first element of the pair which we maintain via the boolean value firstElemOfPair. If its true, then first becomes that value. Otherwise, we know that we’re looking at the second element so we update the diff which is basically that value subtract first. Notice that if we look at a pair in our example as (2,4), we would pick 2 and the diff would be 2. This needs to be subtracted from our sum, hence the reason to maintain both of them. At the end, we finally subtract sum and diff and divide the result by 2 because we were doubling our diff’s too.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public int arrayPairSum(int[] nums) {
boolean[] seen = new boolean[20001];
int sum = 0;
for (int n: nums) {
seen[n + 10000] = !seen[n+10000];
sum += n;
}
int diff = 0;
int first = 0;
boolean firstElemOfPair = true;
for (int i = 0; i < seen.length; ++i) {
if (seen[i]) {
if (firstElemOfPair)
first = i;
else
diff += i-first;
firstElemOfPair = !firstElemOfPair;
}
}
return (sum-diff)/2;
}
|
Runtime: 1 ms, faster than 100.00% of Java online submissions for Reshape the Matrix.
Memory Usage: 38.4 MB, less than 100.00% of Java online submissions for Reshape the Matrix.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public int[][] matrixReshape(int[][] nums, int r, int c) {
int numsR = nums.length; // Get rows and col of nums
int numsC = nums[0].length;
if (numsR * numsC != r*c || (numsR == r && numsC == c)) // If can't reshape or problems
return nums; // asks to reshape in the same dimensions, return the same array
int[][] mat = new int[r][c]; // New matrix to be returned
int row = 0, col = 0, nR = 0, nC = 0; // To keep track of which element to consume and where to place it in the new matrix
while (row != r) {
mat[row][col++] = nums[nR][nC++]; // Increment only the column value for both
if (col == c) { // Check if we are at boundary, if so, increment row
col = 0; // and set col to 0 for both cases.
++row;
}
if (nC == numsC) {
nC = 0;
++nR;
}
}
return mat;
}
|
Runtime: 0 ms, faster than 100.00% of Java online submissions for Swap Nodes in Pairs.
Memory Usage: 34.5 MB, less than 100.00% of Java online submissions for Swap Nodes in Pairs.
The idea is simple. We add a dummy node in front for simplicity as it allows us to generalize the concept of getting two nodes at a time. We maintain a current pointer that points to the node in the actual LinkedList. Then, we get it’s next and it’s next.next and store it into n1 and n2. Now notice that before making n2’s next = n1, we need to store n2’s next into n1’s next. After we do that, we need to make sure that current’s next is n2 which is now working with the actual LinkedList. Then, we need to make sure that current.next.next is n1 which we just fixed and update current which is basically n1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public ListNode swapPairs(ListNode head) {
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode curr = dummy;
while (curr.next != null && curr.next.next != null) {
ListNode n1 = curr.next;
ListNode n2 = n1.next;
n1.next = n2.next;
curr.next = n2;
curr.next.next = n1;
curr = curr.next.next;
}
return dummy.next;
}
|
Iterative Approach 1: This one is very slow.
Runtime: 4 ms, faster than 8.87% of Java online submissions for Generate Parentheses.
Memory Usage: 36.1 MB, less than 100.00% of Java online submissions for Generate Parentheses.
The idea is simple. We basically do a BFS and keep track of the parentheses combination we have obtained so far. Poll the queue and check if it’s length is 2*n (for a given n, we would have # of open brackets = # of closed brackets), add it to the list and check next combination. If not, then check if we can add an open bracket, add it and update number of open bracket count and add this combination to the queue. Then try to see if we can add a closed bracket, if you can add it, then update closed bracket count add that combination to the queue. Keep doing this until the queue becomes empty. This is the first approach I came up with which is naive as you can see since it’s doing an exhaustive search for all valid combination.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| private class Node {
private String data;
private int open;
private int close;
Node(String s, int o, int c) {
data = s;
open = o;
close = c;
}
}
public List<String> generateParenthesis(int n) {
List<String> list = new LinkedList<>();
Queue<Node> q = new LinkedList<>();
q.add(new Node("(", 1, 0));
while (!q.isEmpty()) {
Node u = q.poll();
if (u.data.length() == 2*n)
list.add(u.data);
else {
Node n1 = new Node(u.data, u.open, u.close);
Node n2 = new Node(u.data, u.open, u.close);
if (n1.open < n) {
n1.data = u.data + '(';
++n1.open;
q.add(n1);
}
if (n2.close < u.open) {
n2.data = u.data + ')';
++n2.close;
q.add(n2);
}
}
}
return list;
}
|
Recursive Solution 2: This one is much more faster. I generalized the above idea into the fact that I am adding only valid combinations and any invalid combinations are automatically discarded. The logic is as follows: We know for a given n, the string length should be 2*n. So that forms our base case for recursion, if the length of String s is 2n, we want to add it to the list. Otherwise, we check if the number of open brackets we have so far is less than n. If so, we can add an open bracket. Then check if number of close bracket is less than open, if so that sequence would be valid and add a close bracket and recurse.
Runtime: 1 ms, faster than 95.16% of Java online submissions for Generate Parentheses.
Memory Usage: 36.1 MB, less than 100.00% of Java online submissions for Generate Parentheses.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public List<String> generateParenthesis(int n) {
List<String> list = new ArrayList<>();
helper(list, "(", 1, 0, n);
return list;
}
private void helper(List<String> list, String s, int open, int close, int n) {
if (s.length() == 2*n)
list.add(s);
else {
if (open < n)
helper(list, s+'(', open+1, close, n);
if (close < open)
helper(list, s+')', open, close+1, n);
}
}
|
###Distribute Candies
Pretty simple solution. We want to give maximize the number of unique candies to give to the sister. So we maintain a hashset to collect all the unique candies first. Both of them get half the candies, so let s = number of candies they get. Now, if the size of the set is greater than or equal to s, then the sister only gets s candies out of it. Otherwise, the maximum amount of unique candies she can get is equal to the set size.
1
2
3
4
5
6
7
| public int distributeCandies(int[] candies) {
Set<Integer> set = new HashSet<>(candies.length);
for (int i: candies)
set.add(i);
int share = candies.length/2;
return set.size() >= share ? share: set.size();
}
|
Credits for this simplistic solution to LeetCode user mzchen. The approach is very clever. Notice that if this problem was about finding maximum sum subarray, then a negative number would break the contiguous array. Here, what it does is that it makes our maximum product minimum when we see a negative number and vice versa. We keep track of maximum and minimum we have so far and check if we have a negative number. If so swap our max and min. Then, find the local maximum and minimum between current number and multiplying that number with our current max or min. After that, update our global max value and keep doing this for all values in the array.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public int maxProduct(int[] nums) {
int max = nums[0];
for (int i = 1, imax = max, imin = max; i < nums.length; ++i) {
if (nums[i] < 0) {
int temp = imax;
imax = imin;
imin = temp;
}
imax = Math.max(nums[i], imax * nums[i]);
imin = Math.min(nums[i], imin * nums[i]);
max = Math.max(max, imax);
}
return max;
}
|
Runtime: 1 ms, faster than 95.45% of Java online submissions for Binary Tree Right Side View.
Memory Usage: 36.3 MB, less than 100.00% of Java online submissions for Binary Tree Right Side View.
This is an interesting problem cause initially, I thought we would always have a complete binary tree and I made my initial solution oriented towards it. But then I saw that it doesn’t say that anywhere and it could be any kind of binary tree. So it got me thinking towards a more generalized approach. Notice that to get a right side view of the binary tree, we only need the last value at any given level and put it into the list. So we maintain a queue and also the number of elements we enqueue at each stage. Initially, we put the root node in our queue and our enqueue count is 1. We dequeue exactly that many elements and again enqueue each of those dequeued node’s children. Notice that I am using the variable newEnqueued to keep track of newly enqueued elements. Lastly, we need to check if we dequeued the last element. If so, that must be a part of the solution since it has to be the rightmost element at that level, so I add it to the list. Update enqueued to the new value and repeat until our queue isn’t empty.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public List<Integer> rightSideView(TreeNode root) {
List<Integer> list = new ArrayList<>();
if (root == null)
return list;
Queue<TreeNode> q = new LinkedList<>();
q.add(root);
int enqueued = 1;
while (!q.isEmpty()) {
int newEnqueued = 0;
for (int i = 0; i < enqueued; ++i) {
TreeNode u = q.poll();
if (u.left != null) {
q.add(u.left);
++newEnqueued;
}
if (u.right != null) {
q.add(u.right);
++newEnqueued;
}
if (i == enqueued-1)
list.add(u.val);
}
enqueued = newEnqueued;
}
return list;
}
|
Runtime: 0 ms, faster than 100.00% of Java online submissions for Find Minimum in Rotated Sorted Array.
Memory Usage: 38.6 MB, less than 77.27% of Java online submissions for Find Minimum in Rotated Sorted Array.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public int findMin(int[] nums) {
if (nums.length == 1) // Base case.
return nums[0];
int left = 0;
int right = nums.length-1;
int mid;
while (nums[left] > nums[right]) { // While we are in the ascending order half,
mid = (left + right)/2; // Find the middle element
if (nums[mid] >= nums[left]) // If mid element >= left element, then our min
left = mid + 1; // must be in the right half.
else
right = mid; // otherwise min in the left half.
}
return nums[left]; // left points to minimum element.
}
|
Runtime: 15 ms, faster than 99.74% of Java online submissions for Binary Search Tree Iterator.
Memory Usage: 49.9 MB, less than 93.83% of Java online submissions for Binary Search Tree Iterator.
Logic is same as your In-Order traversal of any Binary Tree, but store the node values you visit in any data structure. Here I am using an ArrayList for storing each of the visited node’s value. Maintain idx value to keep track of which value to return. hasNext() method returns true as long as idx < list.size().
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class BSTIterator {
private List<Integer> list;
private int idx = 0;
public BSTIterator(TreeNode root) {
list = new ArrayList<>();
traverse(root);
}
private void traverse(TreeNode node) {
if (node == null)
return;
traverse(node.left);
list.add(node.val);
traverse(node.right);
}
/** @return the next smallest number */
public int next() {
return list.get(idx++);
}
/** @return whether we have a next smallest number */
public boolean hasNext() {
return idx != list.size();
}
}
|
This question was asked to me for my internship at Yahoo! The idea is simple, we want any one of the peak. So to achieve O(log n) time, we have to mimic binary search algorithm. We look at the middle element and check it’s neighbor, if it’s greater than the middle element, then we know we will have atleast one peak on the right side. Why? Think what could happen. We know that the element next to middle is greater than it, so there are two possibilities on the right side, either elements keep increasing to the right of the middle’s next element or we might go up till a particular index and then go down. So in any case, we will have a peak on the right side. On the other case, if the element on the right side is smaller than the middle, then we know that the left half including the middle will have the peak cause middle is already greater than middle’s right, so we might have middle as the peak itself.
1
2
3
4
5
6
7
8
9
10
11
12
13
| public int findPeakElement(int[] nums) {
if (nums.length == 1)
return 0;
int low = nums[0], high = nums.length - 1, mid;
while (low < high) {
mid = (low + high)/2;
if (nums[mid] < nums[mid+1])
low = mid+1;
else
high = mid;
}
return low;
}
|
Runtime: 0 ms, faster than 100.00% of Java online submissions for Next Permutation.
Memory Usage: 40.3 MB, less than 47.00% of Java online submissions for Next Permutation.
This one was quite interesting in the sense it seems difficult but is very simple once you try out a few example. If we want to find the next lexicographical greater number, then we need to find a particular index from the right side of the array such that the number after it is greater than itself, because by swapping them would give us a next larger number. So what I first do is find the index of the number such that num[idx] > num[idx-1]. We know at this point that all the numbers after that index are reverse sorted, so we need to fix it and sort them in increasing order because lexicographical order demands all the numbers in increasing manner. Example, say nums = [2,3,1,4,2,1,0]. You can see that that the next number should be [2,3,2,0,1,1,4]. Notice that I replaced the number at index 2 with the first number which is greater than it if the array after index 2 was sorted. This gaurantees us a larger lexicographical number. So the first while loop finds us that index number and then I reverse the array after it. Once you reverse it, we should expect the nums array to look like [2,3,1,0,1,2,4]. Note that now we need to find the number larger than the number at index 2, which is 1 in this case. The first number greater than 1 is 2, so the second while loop finds it and then we simply swap them to give us the next larger lexicographically greater number => [2,3,2,0,1,1,4].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| public void nextPermutation(int[] nums) {
if (nums.length < 2)
return;
int idx = nums.length-1;
while (idx > 0 && nums[idx] <= nums[idx-1])
--idx;
reverse(nums, idx);
if (idx == 0)
return;
int val = nums[idx-1];
int i = idx;
while (i < nums.length && nums[i] <= val)
++i;
swap(nums, i, idx-1);
}
private void swap(int[] arr, int idx1, int idx2) {
int temp = arr[idx1];
arr[idx1] = arr[idx2];
arr[idx2] = temp;
}
private void reverse(int[] arr, int start) {
int end = arr.length-1;
while (start < end)
swap(arr, start++, end--);
}
|
The idea is same as binary search except you need to keep track of which half to stay in. We compute the middle index and the value at that index. If the middle value is the target, then return that index. Otherwise, find the correct half. If the number on the left side is < middle value then we know that between the left and middle index, values are increasing. We only need to now check if target is < middle value, if so we need to adjust our right pointer otherwise adjust the left pointer. If left value is not < middle value then we are at a shift where the array is pivoted. We again need to confirm now which half to take. There would be some index i such that nums[left] > nums[i] < nums[mid] and value are increasing upto i and shifts from index i onwards. In this case, we again need to adjust our index pointers and we repeat this loop until left <= right
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public int search(int[] nums, int target) {
int left = 0, right = nums.length-1;
while (left <= right) {
int mid = (left + right)/2;
int midVal = nums[mid];
if (target == midVal)
return mid;
else if (nums[left] <= midVal) {
if (target < midVal && target >= nums[left])
right = mid - 1;
else
left = mid + 1;
}
else {
if (target > midVal && target <= nums[right])
left = mid+1;
else
right = mid - 1;
}
}
return -1;
}
|
Pretty straightforward. Create matrix B of opposite dimensions to those of A. We maintain br and bc which tracks row and columns of B. We iterate over each element of A and put it in B[br][bc] and then ideally we would increment bc for an exact copy, but since we want transpose, we increment br and then reset it to 0 if we fill all the values in a row and increment column count, giving us the tranpose of the matrix.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public int[][] transpose(int[][] A) {
int[][] B = new int[A[0].length][A.length];
int br = 0, bc = 0;
for (int i = 0; i < A.length; ++i) {
for (int j = 0; j < A[0].length; ++j) {
B[br][bc] = A[i][j];
if (++br == B.length) {
br = 0;
++bc;
}
}
}
return B;
}
|
This was an onsite interview question at ThousandEyes. The idea is simple. Basically, we have multiple sorted lists so we have access to one value at a time, that is head of the lists initially and the consecutive nodes. So we need to fetch the minimum element out of all of them in constant time. The easiest way for us to do this is to use a PriorityQueue and define the logic of comparision of two ListNodes. Then, we add all the nodes inside the PQ and build our resulting List. Fetch the minimum valued ListNode and add it to our list. Then we also need to update that particular list’s head, so we add that list’s next in the PQ so the next time it is fetched, we fetch the correct node of the list. Repeat this until the list is empty and return dummy’s next node.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public ListNode mergeKLists(ListNode[] lists) {
if (lists.length == 0)
return null;
PriorityQueue<ListNode> pq = new PriorityQueue<>(lists.length, (n1, n2) -> n1.val - n2.val);
for (ListNode ln: lists)
if (ln != null)
pq.add(ln);
if (pq.isEmpty())
return null;
ListNode node = new ListNode(-1);
ListNode ret = node;
while (!pq.isEmpty()) {
node.next = pq.poll();
node = node.next;
if (node.next != null)
pq.add(node.next);
}
return ret.next;
}
|

